Defining New Functions

在上一讲中我们通过原始表达式，将一个名字和数据绑定起来，我们称这个名字标识符为变量（variable），而通过一些组合的方法，我们可以利用这些变量处理一些复杂的数值操作。

现在我们学习函数定义（function definitions），这是一种更强大的抽象技术，通过这种技术，可以将名称绑定到复合操作，然后可以将其作为一个单元进行引用。 诚然我们可以用这种简单的组合方法去求解很多问题，但是当问题规模上升的时候，我们可能需要复用这些组合的方法，这时候我们就需要对这一系列的过程进行抽象，我们称这种为这种复合操作提供抽象的方法叫做函数。下面我们从一个略显复杂的例子开始，逐步去领会抽象这种方法的威力。

---

如何定义函数？ 函数定义由一个 def 语句组成，该语句指示一个 name ^[1] 和逗号分隔的命名 formal parameters 列表，然后是一个 return 语句，称为函数体，指定了函数的 <return expression> ，它是一个表达式，每当函数被应用时都会被求值：

def <name>(<formal parameters>):
    return <return expression>

需要注意的是第二行必须要缩进（python 的语法），大多数程序员使用四个空格进行缩进。返回的表达式不会立即被求值；它作为新定义函数的一部分存储，只有当函数最终被应用时才会被使用。

---

我们以计算平方根为例，我们在数学上把平方根函数定义为：

$$\sqrt{x}=they,suchthaty\ge 0and{y}^2=x$$

这描述了一个完全合法的数学函数。我们可以使用它来识别一个数是否是另一个数的平方根，或者推导关于平方根的一般事实。另一方面，这个定义并不描述一个过程。事实上，它几乎没有告诉我们如何实际找到一个给定数的平方根。将这个定义重新表述为伪代码也不会有帮助。

（数学上的）函数和过程之间的对比反映了描述事物属性和描述如何做事情之间的一般区别，或者有时候所说的声明性知识和命令性知识之间的区别。在数学中，我们通常关注声明性（是什么）描述，而在计算机科学中，我们通常关注命令性（怎么做）描述。

那我们要如何计算平方根呢？最常见的方法是使用牛顿迭代法。牛顿迭代法的核心在于通过不断重复改进猜测值，直到猜测值满足精度要求，从而得到一个近似的平方根。比如，如果对 x 的平方值有一个猜测 y，那么就可以执行一个简单操作得到一个更好的猜测值：只需要求出 y 和 x/y 的平均值。

我们先来看一个牛顿迭代法求平方根的例子。

Iteration	Current Guess	Improve Guess Calculation	New Guess	Is Good Enough (precision=0.00001)
1	1.0	(1.0 + 2 / 1.0) / 2 = 1.5	1.5	False
2	1.5	(1.5 + 2 / 1.5) / 2 ≈ 1.4167	1.4167	False
3	1.4167	(1.4167 + 2 / 1.4167) / 2 ≈ 1.4142	1.4142	False
4	1.4142	(1.4142 + 2 / 1.4142) / 2 ≈ 1.4142	1.4142	True

我们可以用下面的 python 代码去实现它。

def square(x):
    """
    Returns the square of a given number.

    Parameters:
    x (float): The number to be squared.

    Returns:
    float: The square of the input number.
    """
    return x * x

def average(x, y):
    """
    Returns the average of two numbers.

    Parameters:
    x (float): The first number.
    y (float): The second number.

    Returns:
    float: The average of the two input numbers.
    """
    return (x + y) / 2

def improve_guess(guess, x):
    """
    Improves the guess for the square root of a number using Newton's method.

    Parameters:
    guess (float): The current guess for the square root.
    x (float): The number for which the square root is being calculated.

    Returns:
    float: The improved guess for the square root.
    """
    return average(guess, x / guess)

def is_good_enough(guess, x, precision=0.00001):
    """
    Checks if the guess is good enough for the square root of a number.

    Parameters:
    guess (float): The current guess for the square root.
    x (float): The number for which the square root is being calculated.
    precision (float, optional): The desired precision for the square root. Defaults to 0.00001.

    Returns:
    bool: True if the guess is good enough, False otherwise.
    """
    return abs(square(guess) - x) < precision

def sqrt_newton(x, initial_guess=1.0, precision=0.00001):
    """
    Calculates the square root of a number using Newton's method.

    Parameters:
    x (float): The number for which the square root is being calculated.
    initial_guess (float, optional): The initial guess for the square root. Defaults to 1.0.
    precision (float, optional): The desired precision for the square root. Defaults to 0.00001.

    Returns:
    float: The square root of the input number.
    """
    guess = initial_guess
    if is_good_enough(guess, x, precision):
        return guess
    else:
        guess = improve_guess(guess, x)

不过不要紧张，这个例子乍看上去有些吓人 （确实挺吓人的如果我是个初学者我也会看的头晕） ，但是在我们逐步拆解这些过程后，就能发现这些复杂的操作后面蕴含的是那些最基本的操作。而利用抽象这一强大的武器，我们可以隐去大量的复杂的细枝末节的操作，只关注当前我们需要的东西。

我们先用自然语言描述一个牛顿迭代法求平方根的过程，再接着用程序的语言去实现这一计算过程。 开始时，我们有被开方数的值、一个猜测值和一个精度要求。如果猜测值足够好（满足精度要求）了，我们就完成了这个开方的任务，如果不然，我们就需要重复这一计算过程改进猜测值，事实上，我们要求得就是这个‘猜测值’。于是我们得到了下面这个函数：

def sqrt_newton(x, initial_guess=1.0, precision=0.00001):
    guess = initial_guess
    if is_good_enough(guess, x, precision):
        return guess
    else:
        guess = improve_guess(guess, x)

在这个程序中，我们暂时假设 is_good_enough 和 imporve_guess 这两个函数已经定义好了，我们也暂时不需要考虑它们这两个函数是如何实现的。 我们可以发现它从一个初始猜测值 1.0 开始，计算改进后的猜测值，：判断改进后的猜测值是否足够接近实际值（根号 2）。如果满足精度要求（即差值小于 0.00001），则停止计算；否则，继续改进猜测值。不断重复改进猜测和检查精度的步骤，直到猜测值足够接近根号 2。 把这两个函数作为一个抽象壁垒，我们便暂时可以不用关心具体的实现细节，只需要知道这个过程需要改进猜测值，直到满足精度要求。而把 sqrt_newton 作为一个黑盒子，我们只需要调用它，传入被开方数的值和精度要求，它就会返回根号 2 的数值解，至于里面的细节，我们使用的时候不用关心，只要它的表现是正确的。这就是函数抽象带给我们的便利。

接着我们来对如何完成改进猜测值的过程进行一个快速的看（如果看不懂其实可以先跳过）：

def improve_guess(guess, x):
    return average(guess, x / guess)

def average(x, y):
    return (x + y) / 2

def is_good_enough(guess, x, precision=0.00001):
    return abs(square(guess) - x) < precision

实际上这个 is_good_enough 并不是一个非常好的测试^[2]。 上面这个函数的含义是改进猜测值，直到它足够接近，使得它的平方与被开方数相差小于预定的公差（这里为 0.00001）： sqrt_newton 是我们定义为一组相互定义的程序的第一个示例。注意这个函数的定义是递归的；也就是说，该程序是以自身为基础进行定义的。能够用自身来定义一个程序的这个概念可能会让人感到不安。我们目前 + 可能不清楚这样一个 "循环" 的定义是如何有意义的，更不用说指定一个由计算机执行的定义明确的过程了。这个问题会在后续章节中更详细地讨论。但首先让我们考虑 sqrt 示例所阐明的其他一些重要观点。 我们可以看到计算平方根的问题自然地分解成了一系列子问题：如何判断猜测是否足够接近、如何改进猜测等等。每个任务都是由一个单独的过程来完成的。整个 sqrt 程序可以被看作是一组过程的集合（如图 1.2 所示），这反映了将问题分解为子问题的过程。

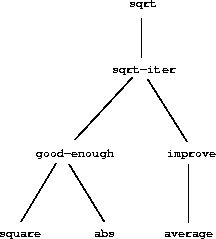
这种分解策略的重要性并不仅仅在于将程序分解成部分。毕竟，我们可以把任何大型程序分解成部分 —— 前十行，接下来的十行，再接下来的十行，依此类推。重要的是每个过程都完成一个可识别的任务，可以用作定义其他过程的模块。 例如，当我们根据 square 定义 is_good_enough 函数时，我们能够将 square 过程视为 “黑盒子”。此时我们并不关心该过程如何计算其结果，只关心它计算平方的事实。计算平方的具体细节可以被抑制，稍后再考虑。事实上，在 is_good_enough 过程看来， square 不是一个完全的过程，而是一个过程的抽象，一种所谓的过程抽象 (Procedure Abstraction)。在这个抽象层次上，任何能够计算平方的过程都是一样的。 因此，如果仅仅考虑函数的返回值，以下两个函数应该是无法区分的，每个函数都接受一个数字作为参数，并产生该数字的平方值.

def square(x):
    return x * x

def square_2(x):
    return pow(x, 2)

我们从这个例子可以看出一个过程定义（函数）应该要封装 / 隐藏掉一些细节。这使得用户在使用一个函数时，不需要完全弄清它是如何实现的，python 的库帮我们封装了很多已经实现好的函数，我们在应用这些库函数时甚至可以完全不需要知道它们的细节，而是专注于我们当前需要实现的功能。这一层函数抽象能够极大的降低程序的复杂性，在后面的学习中我们不可避免地会遇到各种不管是基于程序规模或是程序逻辑本身的复杂性，而如何处理这些复杂性会成为一个很棘手的挑战 我们可以在深度学习 / 爬虫 / 数据分析等各种领域看到这些库，python 简洁的语法和丰富的库函数使它成为了一门很强大的 “胶水语言”。

---

函数是所有程序的基本组成部分，无论大小，都是用来表达编程语言中的计算过程的主要媒介。到目前为止，我们已经讨论了函数的形式属性以及它们的应用方式。现在，我们转向讨论好的函数具备什么特质。从根本上讲，好的函数的特质都强调了函数是抽象的想法。

• 每个函数应该有且只有一个职责。该职责应该使用一个简短的名称来标识，并且可以用一行文本来描述。连续执行多个任务的函数应该被拆分成多个函数。
• 不要重复已经做过的工作是软件工程的核心原则。所谓的 DRY（Don't repeat yourself） 原则指出，多个代码片段不应描述冗余逻辑。相反，这种逻辑应该被实现一次，赋予一个名称，然后多次应用。如果你发现自己在复制和粘贴一块代码，你可能已经找到了进行功能抽象的机会。
• 函数应该被普遍地定义。平方在 Python 库中没有精确定义，因为它是 pow 函数的特殊情况， pow 函数可以将数字提升到任意幂次。

这些准则提高了代码的可读性，减少了错误的数量，并经常减少了编写的总代码量。将复杂的任务分解为简洁的功能是一项需要经验来掌握的技能。幸运的是，Python 提供了几个功能来支持你的努力。

除此之外，需要额外说明的是函数定义会包括描述函数的文档，称为文档字符串，必须与函数体一起缩进。文档字符串通常是三引号。第一行在一行中描述函数的作用。接下来的行可以描述参数并澄清函数的行为。

def pressure(v, t, n):
    """Compute the pressure in pascals of an ideal gas.

    Applies the ideal gas law: http://en.wikipedia.org/wiki/Ideal_gas_law

    v -- volume of gas, in cubic meters
    t -- absolute temperature in degrees kelvin
    n -- particles of gas
    """
    k = 1.38e-23  # Boltzmann's constant
    return n * k * t / v

在编写 Python 程序时，对于除了最简单的函数之外，都要包含文档字符串。请记住，代码只有写一次，但往往会被多次阅读。Python 文档包括文档字符串指南，以确保在不同的 Python 项目中保持一致性。 在 Python 中，注释可以附加在后面跟着 # 符号的行的末尾。例如，上面的注释 Boltzmann's constant 描述了 k 。这些注释不会出现在 Python 的 help 中，解释器会忽略它们。它们是给人类（也许还有大模型）看的。

定义通用函数的一个结果是引入额外的参数。具有许多参数的函数可能难以调用并且难以阅读。 在 Python 中，我们可以为函数的参数提供默认值。在调用该函数时，带有默认值的参数是可选的。如果它们没有提供，那么默认值将绑定到形式参数名上。例如，如果一个应用程序通常对一个摩尔粒子计算压力，这个值可以作为默认值提供：

def pressure(v, t, n=6.022e23):
    """Compute the pressure in pascals of an ideal gas.

    v -- volume of gas, in cubic meters
    t -- absolute temperature in degrees kelvin
    n -- particles of gas (default: one mole)
    """
    k = 1.38e-23  # Boltzmann's constant
    return n * k * t / v

在这个例子中， = 符号根据它的上下文，有着两种不同的意义。在 def 语句头中， = 不执行赋值操作，而是指示在调用 pressure 函数时使用的默认值。相比之下，在函数体中对 k 的赋值语句将名字 k 绑定到玻尔兹曼常数的近似值。 pressure 函数被定义为接受三个参数，但在上述第一次调用表达式中只提供了两个参数。在这种情况下，n 的值来自于 def 语句的默认值。如果提供了第三个参数，则会忽略默认值。 作为准则，函数体中使用的大多数数据值都应表示为命名参数的默认值，以便于检查并且可以被函数调用者更改。一些永远不会更改的值，例如基本常数 k ，可以在函数体中或全局框架中绑定。

---

---

1. 函数推荐的命名风格：

   1. 函数名使用小写字母，单词之间使用下划线分隔。推荐使用描述性的命名。
   2. 参数名称均为小写，用下划线分隔单词。我们更倾向使用单个单词。
   3. 参数名称应该呼应参数在函数中的作用，而不仅仅是允许的参数类型。
   4. 当单个字母参数的作用很明显时，可以接受使用单个字母参数名，但应避免使用 "l"（小写 "ell"）、"O"（大写 "oh"）或 "I"（大写 "i"）以避免与数字混淆。
   ↩︎

2. The is_good-enough test used in computing square roots will not be very effective for finding the square roots of very small numbers. Also, in real computers, arithmetic operations are almost always performed with limited precision. This makes our test inadequate for very large numbers. Explain these statements, with examples showing how the test fails for small and large numbers. An alternative strategy for implementing good-enough? is to watch how guess changes from one iteration to the next and to stop when the change is a very small fraction of the guess. Design a square-root procedure that uses this kind of end test. Does this work better for small and large numbers? ↩︎