C 语言自测标准 —— 链表
链表（单链表）是什么
链表又称单链表、链式存储结构，用于存储逻辑关系为 “一对一” 的数据。
使用链表存储数据，不强制要求数据在内存中集中存储，各个元素可以分散存储在内存中。例如，使用链表存储 {1,2,3}，各个元素在内存中的存储状态可能是：
可以看到，数据不仅没有集中存放，在内存中的存储次序也是混乱的。那么，链表是如何存储数据间逻辑关系的呢？
链表存储数据间逻辑关系的实现方案是：为每一个元素配置一个指针，每个元素的指针都指向自己的直接后继元素，如下图所示：
显然，我们只需要记住元素 1 的存储位置，通过它的指针就可以找到元素 2，通过元素 2 的指针就可以找到元素 3，以此类推，各个元素的先后次序一目了然。像图 2 这样，数据元素随机存储在内存中，通过指针维系数据之间 “一对一” 的逻辑关系，这样的存储结构就是链表。
结点（节点）
在链表中，每个数据元素都配有一个指针，这意味着，链表上的每个 “元素” 都长下图这个样子：
数据域用来存储元素的值，指针域用来存放指针。数据结构中，通常将这样的整体称为结点。
也就是说，链表中实际存放的是一个一个的结点，数据元素存放在各个结点的数据域中。举个简单的例子，图 3 中 {1,2,3} 的存储状态用链表表示，如下图所示：
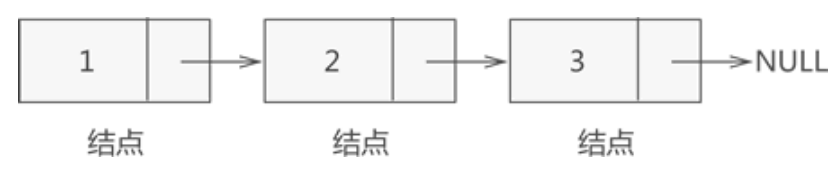
在 C 语言中，可以用结构体表示链表中的结点，例如：
typedef struct Node{
int elem; //代表数据域
struct Node * next; //代表指针域，指向直接后继元素
}Node;
typedef struct Node* Link;头结点、头指针和首元结点
图 4 所示的链表并不完整，一个完整的链表应该由以下几部分构成：
头指针：是指向链表中一个结点所在存储位置的指针。如果链表中有头结点，则头指针指向头结点；若链表中没有头结点，则头指针指向链表中第一个数据结点（也叫首元结点）。
链表有头指针，当我们需要使用链表中的数据时，我们可以使用遍历查找等方法，从头指针指向的结点开始，依次搜索，直到找到需要的数据；反之，若没有头指针，则链表中的数据根本无法使用，也就失去了存储数据的意义。
结点：链表中的节点又细分为头结点、首元结点和其它结点：
头结点：位于链表的表头，即链表中第一个结点，其一般不存储任何数据，特殊情况可存储表示链表信息（表的长度等）的数据。
头结点的存在，其本身没有任何作用，就是一个空结点，但是在对链表的某些操作中，链表有无头结点，可以直接影响编程实现的难易程度。
例如，若链表无头结点，则对于在链表中第一个数据结点之前插入一个新结点，或者对链表中第一个数据结点做删除操作，都必须要当做特殊情况，进行特殊考虑；而若链表中设有头结点，以上两种特殊情况都可被视为普通情况，不需要特殊考虑，降低了问题实现的难度。
链表有头结点，也不一定都是有利的。例如解决约瑟夫环问题，若链表有头结点，在一定程度上会阻碍算法的实现。
所以，对于一个链表来说，设置头指针是必要且必须的，但有没有头结点，则需要根据实际问题特殊分析。
首元结点：指的是链表开头第一个存有数据的结点。
其他节点：链表中其他的节点。
也就是说，一个完整的链表是由头指针和诸多个结点构成的。每个链表都必须有头指针，但头结点不是必须的。
例如，创建一个包含头结点的链表存储 {1,2,3}，如下图所示：
链表的创建
创建一个链表，实现步骤如下：
- 定义一个头指针；
- 创建一个头结点或者首元结点，让头指针指向它；
- 每创建一个结点，都令其直接前驱结点的指针指向它（尾插法 / 头插法）。
创建头指针和头结点（首元结点）
typedef struct Node{
int elem; //代表数据域
struct Node * next; //代表指针域，指向直接后继元素
}Node;
typedef struct Node* Link;
-----------------------------------------------------------------------
Link* head = (Link*)malloc(sizeof(Link)); //创建头指针
*head = (Link)malloc(sizeof(Node));//创建头结点（首元结点）
(*head)->elem = element;//头结点可以不存储数据或存储特殊数据
(*head)->next = NULL;//初始头结点/首元结点的后继元素为空创建结点 —— 头插法
Link p;
while (Judgement) //for 同理
{
p = (Link)malloc(sizeof(Node));
p->elem = element;
p->next = (*head)->next;
(*head)->next = p;
}
创建结点 —— 尾插法
Link p;
Link r = (*head); //临时中间结构指针，在尾插法中始终指向最后一个结点
while (Judgement) //for 同理
{
p = (Link)malloc(sizeof(Node));
p->elem = element;
p->next = NULL;
r->next = p;
r = p;
}
链表的基本操作
学会创建链表之后，本节继续讲解链表的一些基本操作，包括向链表中添加数据、删除链表中的数据、读取、查找和更改链表中的数据。
链表读取元素
获得链表第 i 个数据的算法思路：
- 声明一个结点 p 指向链表的第一个结点，初始化 j 从 1 开始；
- 当 j<i 时，就遍历链表，让 p 的指针向后移动，不断指向下一个结点，j 累加 1；
- 若到链表末尾 p 为空，则说明第 i 个元素不存在；
- 否则读取成功，返回结点 p 的数据
实现代码如下：
#define error 0
#define ok 1
/*用 e 返回 L 中第 i 个数据元素的值*/
int GetElem(Link *L, int i; int *e)
{
Link p;
p = (*L)->next; //p 指向第一个结点
int j = 1;
while (p && j < i) //p 不为空或者计数器 j 还没有等于 i 时，循环继续
{
p = p->next; //p 指向下一个结点
j++;
}
if (!p) //第 i 个元素不存在
return error;
*e = p->elem; //取第 i 个元素的数据
return ok;
}了解了链表如何读取元素，同理我们可以实现更新和查找链表元素。
链表插入元素
向链表中增添元素，根据添加位置不同，可分为以下 3 种情况：
- 插入到链表的头部，作为首元节点；
- 插入到链表中间的某个位置；
- 插入到链表的最末端，作为链表中最后一个结点；
对于有头结点的链表，3 种插入元素的实现思想是相同的，具体步骤是：
- 将新结点的 next 指针指向插入位置后的结点；
- 将插入位置前结点的 next 指针指向插入结点；
例如，在链表 {1,2,3,4} 的基础上分别实现在头部、中间、尾部插入新元素 5，其实现过程如图所示：
从图中可以看出，虽然新元素的插入位置不同，但实现插入操作的方法是一致的，都是先执行步骤 1，再执行步骤 2。实现代码如下：
/*在 L 中第 i 个位置（注意链表中的位置不一定为结点的个数）之前插入新的数据元素 e，
L 的长度加一（可以用头结点存储链表长度）*/
int ListInsert(Link *L, int i, int e)
{
Link p, r; //r 为临时中间结构指针，用于实现插入
p = *L; //p 指向头结点
int j = 1;
while (p && j < i) //寻找第 i 个结点，
{
p = p->next;
j++;
}
if (!p)
return error;
r = (Link)malloc(sizeof(Node));
r->elem = e;
r->next = p->next;
p->next = r;
return ok;
}注意：链表插入元素的操作必须是先步骤 1，再步骤 2；反之，若先执行步骤 2，除非再添加一个指针，作为插入位置后续链表的头指针，否则会导致插入位置后的这部分链表丢失，无法再实现步骤 1。
对于没有头结点的链表，在头部插入结点比较特殊，需要单独实现。
和 2)、3) 种情况相比，由于链表没有头结点，在头部插入新结点，此结点之前没有任何结点，实现的步骤如下：
- 将新结点的指针指向首元结点；
- 将头指针指向新结点。
实现代码如下：
/*在 L 中第 i 个位置（注意链表中的位置不一定为结点的个数）之前插入新的数据元素 e，
L 的长度加一（可以用头结点存储链表长度）*/
int ListInsert(Link *L, int i, int e)
{
if (i == 1)
{
Link r = (Link)malloc(sizeof(Node));
r->elem = e;
r->next = (*L)->next;
*L = r;
}
else
{
//......
}
}链表删除元素
从链表中删除指定数据元素时，实则就是将存有该数据元素的节点从链表中摘除。
对于有头结点的链表来说，无论删除头部（首元结点）、中部、尾部的结点，实现方式都一样，执行以下三步操作：
- 找到目标元素所在结点的直接前驱结点；
- 将目标结点从链表中摘下来；
- 手动释放结点占用的内存空间；
从链表上摘除目标节点，只需找到该节点的直接前驱节点 temp，执行如下操作：
temp->next=temp->next->next;例如，从存有 {1,2,3,4} 的链表中删除存储元素 3 的结点，则此代码的执行效果如图 3 所示：
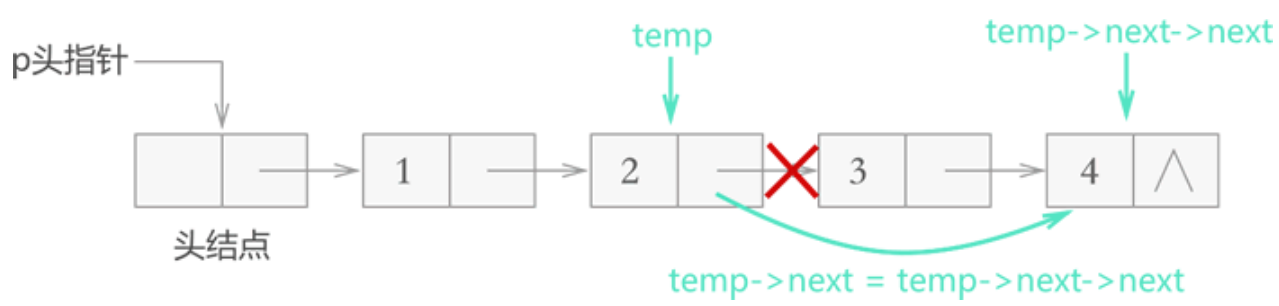
实现代码如下：
/*删除 L 中的第 i 个数据元素，并用 e 返回其值，L 的长度减一
（可以用头结点存储链表长度）*/
int ListDelete(Link *L, int i, int* e)
{
Link p, r;
p = *L;
int j = 1;
while (p->next && j < i) //寻找删除元素中的前驱元素
{
p = p->next;
j++;
}
if (!(p->next))
return error; //L 中不存在第 i 个元素
r = p->next; //标记要删除的结点
p->next = r->next; //移除结点
*e = r->elem; //返回结点所存数据
free(r); //释放结点
return ok;
}对于不带头结点的链表，需要单独考虑删除首元结点的情况，删除其它结点的方式和图 3 完全相同，如下图所示：
实现代码如下：
/*删除 L 中的第 i 个数据元素，并用 e 返回其值，L 的长度减一
（可以用头结点存储链表长度）*/
int ListDelete(Link *L, int i, int* e)
{
if (i == 1)
{
Link r = *L;
*L= r->next;
*e = r->elem;
free(r);
}
else
{
//......
}
}链表查找元素
在链表中查找指定数据元素，最常用的方法是：从首元结点开始依次遍历所有节点，直至找到存储目标元素的结点。如果遍历至最后一个结点仍未找到，表明链表中没有存储该元素。
链表更新元素
更新链表中的元素，只需通过遍历找到存储此元素的节点，对节点中的数据域做更改操作即可。
约瑟夫环
约瑟夫环问题，是一个经典的循环链表问题，题意是：已知 n 个人（分别用编号 1，2，3，…，n 表示）围坐在一张圆桌周围，从编号为 k 的人开始顺时针报数，数到 m 的那个人出列；他的下一个人又从 1 开始，还是顺时针开始报数，数到 m 的那个人又出列；依次重复下去，直到圆桌上剩余一个人。
如图所示，假设此时圆周周围有 5 个人，要求从编号为 3 的人开始顺时针数数，数到 2 的那个人出列：
出列顺序依次为：
- 编号为 3 的人开始数 1，然后 4 数 2，所以 4 先出列；
- 4 出列后，从 5 开始数 1，1 数 2，所以 1 出列；
- 1 出列后，从 2 开始数 1，3 数 2，所以 3 出列；
- 3 出列后，从 5 开始数 1，2 数 2，所以 2 出列；
- 最后只剩下 5 自己，所以 5 胜出。
那么，究竟要如何用链表实现约瑟夫环呢？如何让一个含 5 个元素的约瑟夫环，能从第 5 个元素出发，访问到第 2 个元素呢？上面所讲的链表操作显然是难以做到的，解决这个问题就需要用到循环链表。
循环链表
将单链表中终端结点的指针端由空指针改为指向头结点，使得整个单链表形成一个环，这种头尾相接的单链表成为单循环链表，简称循环链表。
循环链表解决了一个很麻烦的问题。如何从当中一个结点出发，访问到链表的全部结点。
为了使空链表和非空链表处理一致，我们通常设一个头结点，当然，并不是说，循环链表一定要头结点，这需要注意。循环链表带有头结点的空链表如图所示：
对于非空的循环链表如图所示：
循环链表和单链表的主要差异就在于循环的判断条件上，原来是判断 p->next 是否为空，现在则是 p->next 不等于头结点，则循环未结束。