项目：遗传

TIP

我们为你提供了一个简单有趣的项目，帮助你进行知识巩固，请认真阅读文档内容。

如果你卡住了，请记得回来阅读文档，或请求身边人的帮助。

📥

本节附件下载

背景

GJB2 基因的突变版本是导致新生儿听力障碍的主要原因之一。每个人都携带两个版本的基因，因此每个人都有可能拥有 0、1 或 2 个听力障碍版本的 GJB2 基因。不过，除非一个人接受基因测试，否则要知道一个人拥有多少个变异的 GJB2 基因并不那么容易。存在一些 "特殊状态"：我们可以观察到一个人是否听力损伤，但这不一定能直接判断是否有突变基因。毕竟，有些人可能有 1 或 2 个突变的 GJB2 基因，但没有表现出听力障碍，而其他人可能没有突变的 GJB2 基因，但仍然表现出听力障碍。

每个孩子都会从他们的父母那里继承一个 GJB2 基因。如果父母有两个变异基因，那么他们会将变异基因传给孩子；如果父母没有变异基因，那么他们不会将变异基因传给孩子；如果父母有一个变异基因，那么该基因传给孩子的概率为 0.5。不过，在基因被传递后，它有一定的概率发生额外的突变：从导致听力障碍的基因版本转变为不导致听力障碍的版本，或者反过来。

我们可以尝试通过对所有相关变量形成一个贝叶斯网络来模拟所有这些关系，就像下面这个网络一样，它考虑了一个由两个父母和一个孩子组成的家庭。

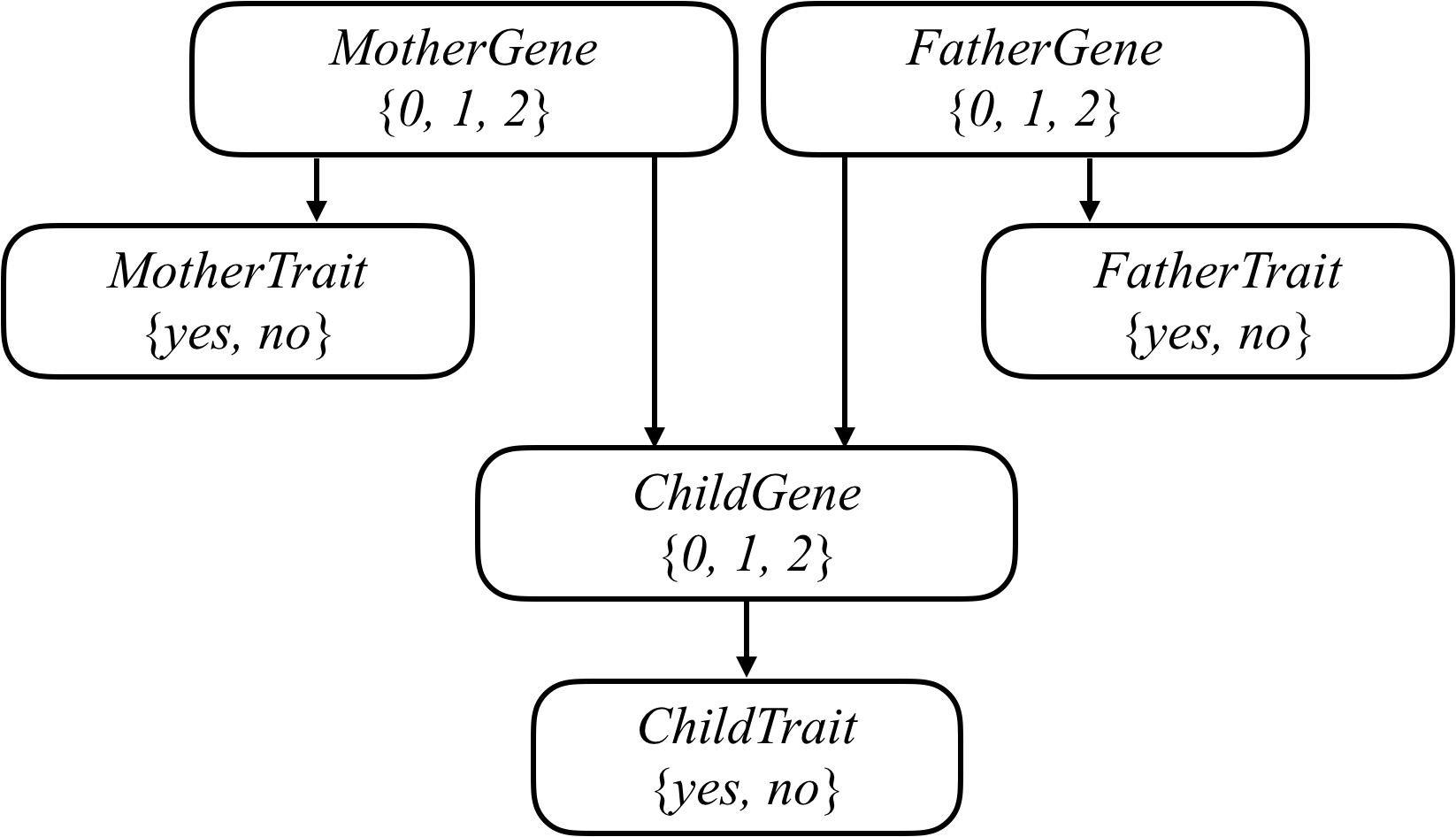
家庭中的每个人都有一个 Gene 随机变量，代表一个人有多少个特定基因： 0、1 或 2 。家族中的每个人也有一个 Trait 随机变量，它是 yes 或 no ，取决于该人是否表达基于该基因的性状（例如，听力障碍）。从每个人的 Gene 变量到他们的 Trait 变量之间有一个箭头，以表示一个人的基因影响他们具有特定性状的概率。同时，也有一个箭头从母亲和父亲的 Gene 随机变量到他们孩子的 Gene 随机变量：孩子的基因取决于他们父母的基因。

你在这个项目中的任务是使用这个模型对人群进行推断。给出人们的信息，他们的父母是谁，以及他们是否具有由特定基因引起的特定可观察特征（如听力损失），你的人工智能将推断出每个人的基因的概率分布，以及任何一个人是否会表现出有关特征的概率分布。

理解

打开 data/family0.csv ，看看数据目录中的一个样本数据集（你可以在文本编辑器中打开，或者在 Google Sheets、Excel 或 Apple Numbers 等电子表格应用程序中打开）。注意，第一行定义了这个 CSV 文件的列： name , mother , father , 和 trait 。下一行表明 Harry 的母亲是 Lily，父亲是 James，而 Trait 的空单元格意味着我们不知道 Harry 是否有这种性状。同时，James 在我们的数据集中没有列出父母（如母亲和父亲的空单元格所示），但确实表现出了性状（如 Trait 单元格中的 1 所示）。另一方面，Lily 在数据集中也没有列出父母，但没有表现出这种性状（如 Trait 单元格中的 0 表示）。

打开 heredity.py ，首先看一下 PROBS 的定义。 PROBS 是一个包含若干常数的字典，代表各种不同事件的概率。所有这些事件都与一个人拥有多少个特定的突变基因，以及一个人是否基于该基因表现出特定的性状有关。这里的数据松散地基于 GJB2 基因的听力障碍版本和听力障碍性状的概率，但通过改变这些值，你也可以用你的人工智能来推断其他的基因和性状！

首先， PROBS["gene"] 代表了该基因的无条件概率分布（即如果我们对该人的父母一无所知的概率）。根据分布代码中的数据，在人群中，有 1% 的机会拥有该基因的 2 个副本，3% 的机会拥有该基因的 1 个副本，96% 的机会拥有该基因的零副本。

接下来， PROBS["trait"] 表示一个人表现出某种性状（如听力障碍）的条件概率。这实际上是三个不同的概率分布：基因的每个可能值都有一个。因此， PROBS["trait"][2] 是一个人在有两个突变基因的情况下具有该特征的概率分布：在这种情况下，他们有 65% 的机会表现出该特征，而有 35% 的机会不表现出该特征。同时，如果一个人有 0 个变异基因，他们有 1% 的机会表现出该性状，99% 的机会不表现出该性状。

最后， PROBS["mutation"] 是一个基因从作为相关基因突变为不是该基因的概率，反之亦然。例如，如果一个母亲有两个变异基因，并因此将其中一个传给她的孩子，就有 1% 的机会突变为不再是变异基因。相反，如果一个母亲没有任何变异基因，因此没有把变异基因传给她的孩子，但仍有 1% 的机会突变为变异基因。因此，即使父母双方都没有变异基因，他们的孩子也可能有 1 个甚至 2 个变异基因。

最终，你计算的概率将以 PROBS 中的这些数值为基础。

现在，看一下 main 函数。该函数首先将数据从一个文件加载到一个字典 people 中。 people 将每个人的名字映射到另一个包含他们信息的字典中：包括他们的名字，他们的母亲（如果数据集中有一个母亲），他们的父亲（如果数据集中有一个父亲），以及他们是否被观察到有相关的特征（如果有则为 True ，没有则为 False ，如果我们不知道则为 None ）。接下来， main 中定义了一个字典 probabilities ，所有的概率最初都设置为 0。这就是你的项目最终要计算的内容：对于每个人，你的人工智能将计算他们有多少个变异基因的概率分布，以及他们是否具有该性状。例如， probabilities["Harry"]["gene"][1] 将是 Harry 有 1 个变异基因的概率，而 probabilities["Lily"]["trait"][False] 将是 Lily 没有表现出该性状的概率。

如果不熟悉的话，这个 probabilities 字典是用 python 字典创建的，在这种情况下，它为我们的 people 中的每个 person 创建一个键 / 值对。

最终，我们希望根据一些证据来计算这些概率：鉴于我们知道某些人有或没有这种特征，我们想确定这些概率。你在这个项目中的任务是实现三个函数来做到这一点： joint_probability 计算一个联合概率， update 将新计算的联合概率添加到现有的概率分布中，然后 normalize 以确保所有概率分布最后和为 1。

明确

完成 joint_probability 、 update 和 normalize 的实现。

joint_probability 函数应该接受一个 people 的字典作为输入，以及关于谁拥有多少个变异基因，以及谁表现出该特征的数据。该函数应该返回所有这些事件发生的联合概率。

该函数接受四个数值作为输入： people , one_gene , two_genes , 和 have_trait 。
- people 是一个在 "理解" 一节中描述的人的字典。键代表名字，值是包含 mother 和 father 键的字典。你可以假设 mother 和 father 都是空白的（数据集中没有父母的信息），或者 mother 和 father 都会指代 people 字典中的其他人物。
- one_gene 是一个集合，我们想计算所有集合元素有一个变异基因的概率。
- two_genes 是一个集合，我们想计算所有集合元素有两个变异基因的概率。
- have_trait 是一个集合，我们想计算所有集合元素拥有该性状的概率。
- 对于不在 one_gene 或 two_genes 中的人，我们想计算他们没有变异基因的概率；对于不在 have_trait 中的人，我们想计算他们没有该性状的概率。
例如，如果这个家庭由 Harry、James 和 Lily 组成，那么在 one_gene = {"Harry"} 、 two_genes = {"James"} 和 trait = {"Harry"、"James"} 的情况下调用这个函数，应该计算出 Lily 没有变异基因、Harry 拥有一个变异基因、James 拥有两个变异基因、Harry 表现出该性状、James 表现出该性状和 Lily 没有表现出该性状的联合概率。
对于数据集中没有列出父母的人，使用概率分布 PROBS["gene"] 来确定他们有特定数量基因的概率。
对于数据集中有父母的人来说，每个父母都会把他们的两个基因中的一个随机地传给他们的孩子，而且有一个 PROBS["mutation"] 的机会，即它会发生突变（从变异基因变成正常基因，或者相反）。
使用概率分布 PROBS["trait"] 来计算一个人具有或不具有形状的概率。

update 函数将一个新的联合分布概率添加到 probabilities 中的现有概率分布中。

该函数接受五个值作为输入： probabilities , one_gene , two_genes , have_trait , 和 p 。
- probabilities 是一个在 "理解" 部分提到的字典。每个人都被映射到一个 "gene" 分布和一个 "trait" 分布。
- one_gene 是一个集合，我们想计算所有集合元素有一个变异基因的概率。
- two_genes 是一个集合，我们想计算所有集合元素有两个变异基因的概率。
- have_trait 是一个集合，我们想计算所有集合元素拥有该性状的概率。
- p 是联合分布的概率。
对于概率中的每个人，该函数应该更新 probabilities[person]["gene"] 分布和 probabilities[person]["trait"] 分布，在每个分布中的适当数值上加上 p 。所有其他数值应保持不变。
例如，如果 "Harry" 同时出现在 two_genes 和 have_trait 中，那么 p 将被添加到 probabilities["Harry"]["gene"][2] 和 probabilities["Harry"]["trait"][True] 。
该函数不应返回任何值：它只需要更新 probabilities 字典。

normalize 函数更新 probabilities 字典，使每个概率分布被归一化（即和为 1，相对比例相同）。

该函数接受一个单一的值： probabilities 。
- probabilities 是一个在 "理解" 部分提到的字典。每个人都被映射到一个 "gene" 分布和一个 "trait" 分布。
对于 probabilities 中每个人的两个分布，这个函数应该将该分布归一化，使分布中的数值之和为 1，分布中的相对数值是相同的。
例如，如果 probabilities["Harry"]["trait"][True] 等于 0.1 ，概率 probabilities["Harry"]["trait"][False] 等于 0.3 ，那么你的函数应该将前一个值更新为 0.25 ，后一个值更新为 0.75 : 现在数字之和为 1，而且后一个值仍然比前一个值大三倍。
该函数不应返回任何值：它只需要更新 probabilities 字典。

除了规范中要求你实现的三个函数外，你不应该修改 heredity.py 中的任何其他东西，尽管你可以编写额外的函数和 / 或导入其他 Python 标准库模块。如果熟悉的话，你也可以导入 numpy 或 pandas ，但是你不应该使用任何其他第三方 Python 模块。

一个联合概率例子

为了帮助你思考如何计算联合概率，我们在下面附上一个例子。

请考虑以下 people 的值：

python

{
  'Harry': {'name': 'Harry', 'mother': 'Lily', 'father': 'James', 'trait': None},
  'James': {'name': 'James', 'mother': None, 'father': None, 'trait': True},
  'Lily': {'name': 'Lily', 'mother': None, 'father': None, 'trait': False}
}

这里我们将展示 joint_probability(people, {"Harry"}, {"James"}, {"James"}) 的计算。根据参数， one_gene 是 {"Harry"} ， two_genes 是 {"James"} ，而 has_trait 是 {"James"} 。因此，这代表了以下的概率：Lily 没有变异基因，不具有该性状；Harry 有一个变异基因，不具有该性状；James 有 2 个变异基因，具有该性状。

我们从 Lily 开始（我们考虑人的顺序并不重要，只要我们把正确的数值乘在一起，因为乘法是可交换的）。Lily 没有变异基因，概率为 0.96 （这就是 PROBS["gene"][0] ）。鉴于她没有变异基因，她没有这个性状的概率为 0.99 （这是 PROBS["trait"][0][False] ）。因此，她没有变异基因且没有该性状的概率是 0.96*0.99=0.9504 。

接下来，我们考虑 James。James 有 2 个变异基因，概率为 0.01 （这是 PROBS["gene"][2] ）。鉴于他有 2 个变异基因，他确实具有该性状的概率为 0.65 。因此，他有 2 个变异基因并且他确实具有该性状的概率是 0.01*0.65=0.0065 。

最后，我们考虑 Harry。Harry 有 1 个变异基因的概率是多少？有两种情况可以发生。要么他从母亲那里得到这个基因，而不是从父亲那里，要么他从父亲那里得到这个基因，而不是从母亲那里。他的母亲 Lily 没有变异基因，所以 Harry 会以 0.01 的概率从他母亲那里得到这个基因（这是 PROBS["mutation"] ），因为从他母亲那里得到这个基因的唯一途径是基因突变；相反，Harry 不会从他母亲那里得到这个基因，概率是 0.99 。他的父亲 James 有 2 个变异基因，所以 Harry 会以 0.99 的概率从他父亲那里得到这个基因（这是 1-PROBS["mutation"] ），但会以 0.01 的概率从他母亲那里得到这个基因（突变的概率）。这两种情况加在一起可以得到 0.99*0.99+0.01*0.01=0.9802 ，即 Harry 有 1 个变异基因的概率。

考虑到 Harry 有 1 个变异基因，他没有该性状的概率是 0.44 （这是 PROBS["trait"][1][false] ）。因此，哈利有 1 个变异基因而没有该性状的概率是 0.9802 * 0.44 = 0.431288 。

因此，整个联合概率是三个人中每个人的所有这些数值相乘的结果： 0.9504 * 0.0065 * 0.431288 = 0.0026643247488 。

提示

回顾一下，要计算多个事件的联合概率，你可以通过将这些概率相乘来实现。但请记住，对于任何孩子来说，他们拥有一定数量的基因的概率是以他们的父母拥有什么基因为条件的。

检查方法

bash

check50 ai50/projects/2024/x/heredity --offline

样例代码

python

import csv
import itertools
import sys

PROBS = {

    # Unconditional probabilities for having gene
    "gene": {
        2: 0.01,
        1: 0.03,
        0: 0.96
    },

    "trait": {

        # Probability of trait given two copies of gene
        2: {
            True: 0.65,
            False: 0.35
        },

        # Probability of trait given one copy of gene
        1: {
            True: 0.56,
            False: 0.44
        },

        # Probability of trait given no gene
        0: {
            True: 0.01,
            False: 0.99
        }
    },

    # Mutation probability
    "mutation": 0.01
}


def main():

    # Check for proper usage
    if len(sys.argv) != 2:
        sys.exit("Usage: python heredity.py data.csv")
    people = load_data(sys.argv[1])

    # Keep track of gene and trait probabilities for each person
    probabilities = {
        person: {
            "gene": {
                2: 0,
                1: 0,
                0: 0
            },
            "trait": {
                True: 0,
                False: 0
            }
        }
        for person in people
    }

    # Loop over all sets of people who might have the trait
    names = set(people)
    for have_trait in powerset(names):

        # Check if current set of people violates known information
        fails_evidence = any(
            (people[person]["trait"] is not None and
             people[person]["trait"] != (person in have_trait))
            for person in names
        )
        if fails_evidence:
            continue

        # Loop over all sets of people who might have the gene
        for one_gene in powerset(names):
            for two_genes in powerset(names - one_gene):

                # Update probabilities with new joint probability
                p = joint_probability(people, one_gene, two_genes, have_trait)
                update(probabilities, one_gene, two_genes, have_trait, p)

    # Ensure probabilities sum to 1
    normalize(probabilities)

    # Print results
    for person in people:
        print(f"{person}:")
        for field in probabilities[person]:
            print(f"  {field.capitalize()}:")
            for value in probabilities[person][field]:
                p = probabilities[person][field][value]
                print(f"    {value}: {p:.4f}")


def load_data(filename):
    """
    Load gene and trait data from a file into a dictionary.
    File assumed to be a CSV containing fields name, mother, father, trait.
    mother, father must both be blank, or both be valid names in the CSV.
    trait should be 0 or 1 if trait is known, blank otherwise.
    """
    data = dict()
    with open(filename) as f:
        reader = csv.DictReader(f)
        for row in reader:
            name = row["name"]
            data[name] = {
                "name": name,
                "mother": row["mother"] or None,
                "father": row["father"] or None,
                "trait": (True if row["trait"] == "1" else
                          False if row["trait"] == "0" else None)
            }
    return data


def powerset(s):
    """
    Return a list of all possible subsets of set s.
    """
    s = list(s)
    return [
        set(s) for s in itertools.chain.from_iterable(
            itertools.combinations(s, r) for r in range(len(s) + 1)
        )
    ]


def joint_probability(people, one_gene, two_genes, have_trait):
    """
    Compute and return a joint probability.

    The probability returned should be the probability that
        * everyone in set `one_gene` has one copy of the gene, and
        * everyone in set `two_genes` has two copies of the gene, and
        * everyone not in `one_gene` or `two_gene` does not have the gene, and
        * everyone in set `have_trait` has the trait, and
        * everyone not in set` have_trait` does not have the trait.
    """
    probability=1.0
    for person in people:
        if people[person]["mother"] is None:
            if person in one_gene:
                probability*=PROBS["gene"][1]
                if person in have_trait:
                    probability*=PROBS["trait"][1][True]
                else:
                    probability*=PROBS["trait"][1][False]
            elif person in two_genes:
                probability*=PROBS["gene"][2]
                if person in have_trait:
                    probability*=PROBS["trait"][2][True]
                else:
                    probability*=PROBS["trait"][2][False]
            else:
                probability*=PROBS["gene"][0]
                if person in have_trait:
                    probability*=PROBS["trait"][0][True]
                else:
                    probability*=PROBS["trait"][0][False]
            
        else:
            num_father=0
            num_mather=0
            if people[person]["mother"] in one_gene:
                num_mather=1
            elif people[person]["mother"] in two_genes:
                num_mather=2
            if people[person]["father"] in one_gene:
                num_father=1
            elif people[person]["father"] in two_genes:
                num_father=2
            pro_father=num_father/2
            pro_mather=num_mather/2
            pro_2=pro_father*pro_mather*(1-PROBS["mutation"])*(1-PROBS["mutation"])+\
                (1-pro_father)*(1-pro_mather)*PROBS["mutation"]*PROBS["mutation"]+\
                    pro_father*(1-pro_mather)*PROBS["mutation"]*(1-PROBS["mutation"])+\
                    pro_mather*(1-pro_father)*PROBS["mutation"]*(1-PROBS["mutation"])
            pro_0=(1-pro_father)*(1-pro_mather)*(1-PROBS["mutation"])*(1-PROBS["mutation"])+\
                pro_father*(1-pro_mather)*(1-PROBS["mutation"])*PROBS["mutation"]+\
                pro_mather*(1-pro_father)*(1-PROBS["mutation"])*PROBS["mutation"]+\
                pro_mather*pro_father*PROBS["mutation"]*PROBS["mutation"]
            pro_1=1-pro_0-pro_2
            if person in one_gene:
                probability*=pro_1
                if person in have_trait:
                    probability*=PROBS["trait"][1][True]
                else:
                    probability*=PROBS["trait"][1][False]
            elif person in two_genes:
                probability*=pro_2
                if person in have_trait:
                    probability*=PROBS["trait"][2][True]
                else:
                    probability*=PROBS["trait"][2][False]
            else:
                probability*=pro_0
                if person in have_trait:
                    probability*=PROBS["trait"][0][True]
                else:
                    probability*=PROBS["trait"][0][False]
    return probability
            




def update(probabilities, one_gene, two_genes, have_trait, p):
    """
    Add to `probabilities` a new joint probability `p`.
    Each person should have their "gene" and "trait" distributions updated.
    Which value for each distribution is updated depends on whether
    the person is in `have_gene` and `have_trait`, respectively.
    """
    for person in probabilities:
        if person in one_gene:
            probabilities[person]["gene"][1]+=p
        elif person in two_genes:
            probabilities[person]["gene"][2]+=p
        else:
            probabilities[person]["gene"][0]+=p
        if person in have_trait:
            probabilities[person]["trait"][True]+=p
        else:
            probabilities[person]["trait"][False]+=p

def normalize(probabilities):
    """
    Update `probabilities` such that each probability distribution
    is normalized (i.e., sums to 1, with relative proportions the same).
    """
    for person in probabilities:
        sum_gene=sum(probabilities[person]["gene"].values())
        sum_trait=sum(probabilities[person]["trait"].values())
        for i in range(3):
            probabilities[person]["gene"][i]/=sum_gene
        for i in range(2):
            probabilities[person]["trait"][i]/=sum_trait


if __name__ == "__main__":
    main()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244

3.6.2搜索

3.6.3知识推理

3.6.4不确定性问题

3.6.5最优化

3.7.2Prerequisites

3.7.3Ray Tracing

3.8.4Numpy&Pytorch系列

3.8.5LLM实操项目

3.8.5.2Atri-微调角色扮演

3.8.5.3AI绘图大模型-Stable Diffusion

3.8.5.4语音识别-Whisper + Gradio部署

3.8.5.5微调Llama 2

项目：遗传

背景

理解

明确

一个联合概率例子

提示

检查方法

样例代码

3.8.5.2Atri-微调角色扮演

3.8.5.3AI绘图大模型-Stable Diffusion

3.8.5.4语音识别-Whisper + Gradio部署

3.8.5.5微调Llama 2

项目：遗传 ​

背景 ​

理解 ​

明确 ​

一个联合概率例子 ​

提示 ​

检查方法 ​

样例代码 ​

项目：遗传

背景

理解

明确

一个联合概率例子

提示

检查方法

样例代码