最优化

最优化是指从一组可能的选项中选择最佳选项。我们已经遇到过试图找到最佳选项的问题，比如在极大极小算法中，今天我们将学习一些工具，可以用来解决更广泛的问题。

局部搜索 (Local Search)

局部搜索是一种保持单一节点并通过移动到邻近的节点进行搜索的搜索算法。这种类型的算法与我们之前看到的搜索类型不同。例如，在解决迷宫的过程中，我们想找到通往目标的最快捷的方法，也就是最佳方法，而通常情况下，局部搜索会带来一个不是最佳但 "足够好" 的答案，以节省计算能力。考虑一下下面这个局部搜索问题的例子：我们有四所房子在设定的位置。我们想建两所医院，使每所房子到医院的距离最小。这个问题可以形象地描述如下：

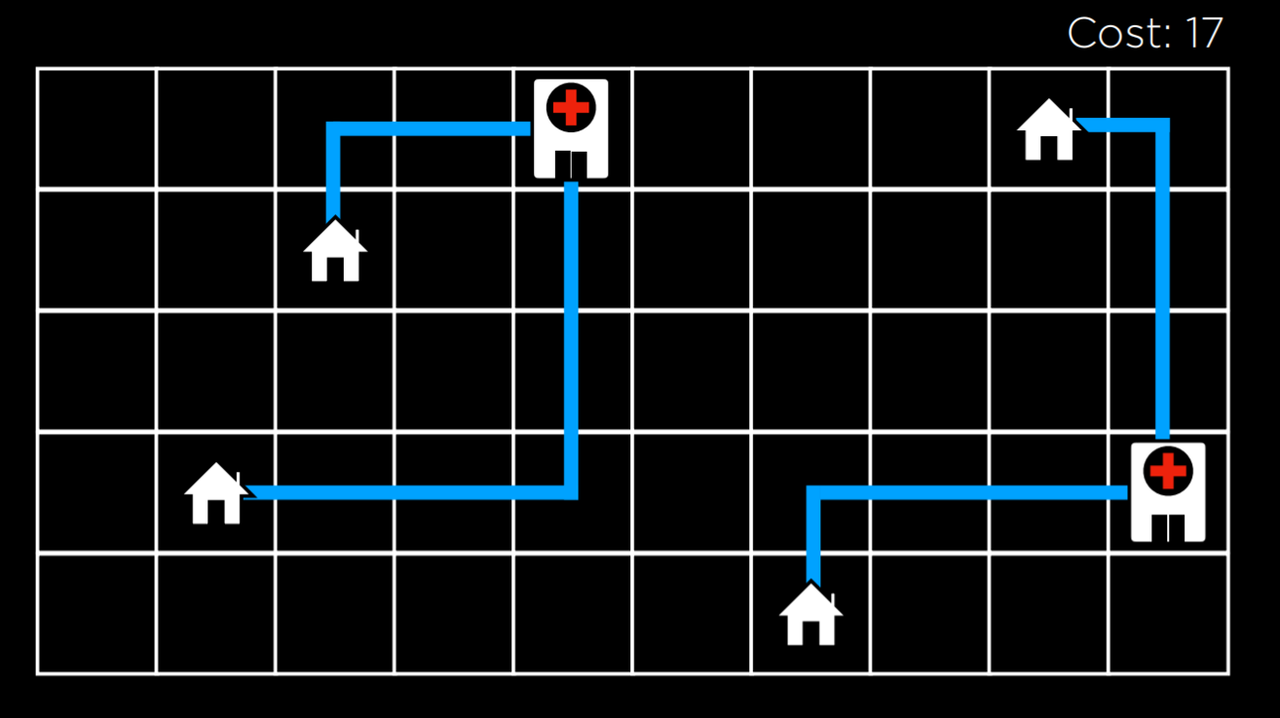
在这幅图中，我们看到的是房屋和医院的可能配置。它们之间的距离是用曼哈顿距离 (向上、向下和向两侧移动的次数；在搜索中详细讨论) 来衡量的，从每个房子到最近的医院的距离之和是 17。我们称其为成本 (cost)，因为我们试图使这个距离最小化。在这种情况下，一个状态将是房屋和医院的任何一个位置分布。

把这个概念抽象化，我们可以把每一种房屋和医院的位置分布表现为下面的状态空间图的横轴。图中的每一条都代表一个状态的值，在我们的例子中，它是该位置分布下房屋和医院配置的成本。

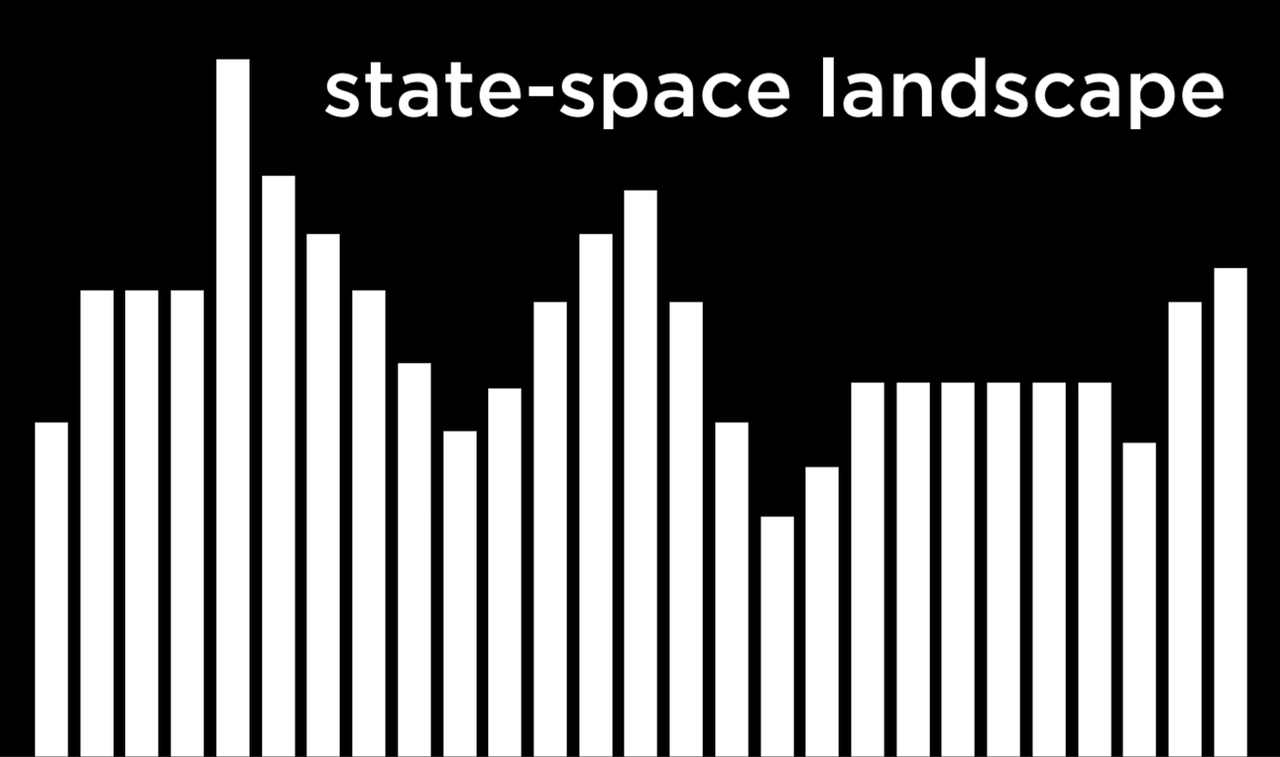
从这个可视化的角度来看，我们可以为我们接下来的讨论定义几个重要的术语：

目标函数 (Objective Function) 是一个函数，我们用它来最大化解决方案的值。
成本函数 (Cost Function) 是一个我们用来最小化解决方案成本的函数 (这就是我们在房屋和医院的例子中要使用的函数。我们想要最小化从房屋到医院的距离)。
当前状态 (Current State) 是指函数目前正在考虑的状态。
邻居状态 (Neighbor State) 是当前状态可以过渡到的一个状态。在上面的一维状态空间图中，邻居状态是指当前状态两侧的状态。在我们的例子中，邻居状态可以是将其中一家医院向任何方向移动一步所产生的状态。邻居状态通常与当前状态相似，因此，其值与当前状态的值接近。

请注意，局部搜索算法的工作方式是考虑当前状态下的一个节点，然后将该节点移动到当前状态的一个邻节点处。这与极大极小算法不同，例如，在极大极小算法中，状态空间中的每一个状态都被递归地考虑。

爬山算法 (Hill Climbing)

爬山算法是局部搜索算法的一种类型。在这个算法中，邻居的状态与当前的状态进行比较，如果其中任何一个状态更好，我们就把当前的节点从当下的状态改为该邻居的状态。“好状态” 的定义是由目标函数决定的，倾向于一个较高的值，或倾向于一个较低的值。

一个爬山算法在伪代码中会有以下样子：

txt

function Hill-Climb(problem):
    current = initial state of problem
    repeat:
        neighbor = best valued neighbor of current
        if neighbor not better than current:
            return current
        current = neighbor

在这个算法中，我们从一个当前状态开始。在一些问题中，我们会知道当前的状态是什么，而在其他问题中，我们将不得不从随机选择一个状态开始。然后，我们重复以下动作：我们评估邻居状态，选择一个具有最佳值的邻居状态。然后，我们将这个邻居状态的值与当前状态的值进行比较。如果邻居状态更好，我们将当前状态切换到邻居状态，然后重复这个过程。当我们将最佳邻居与当前状态进行比较，并且当前状态更好时，该过程就结束了。然后，我们返回当前状态。

使用爬山算法，我们可以开始改进我们在例子中分配给医院的位置。经过几次转换，我们得到了以下状态：

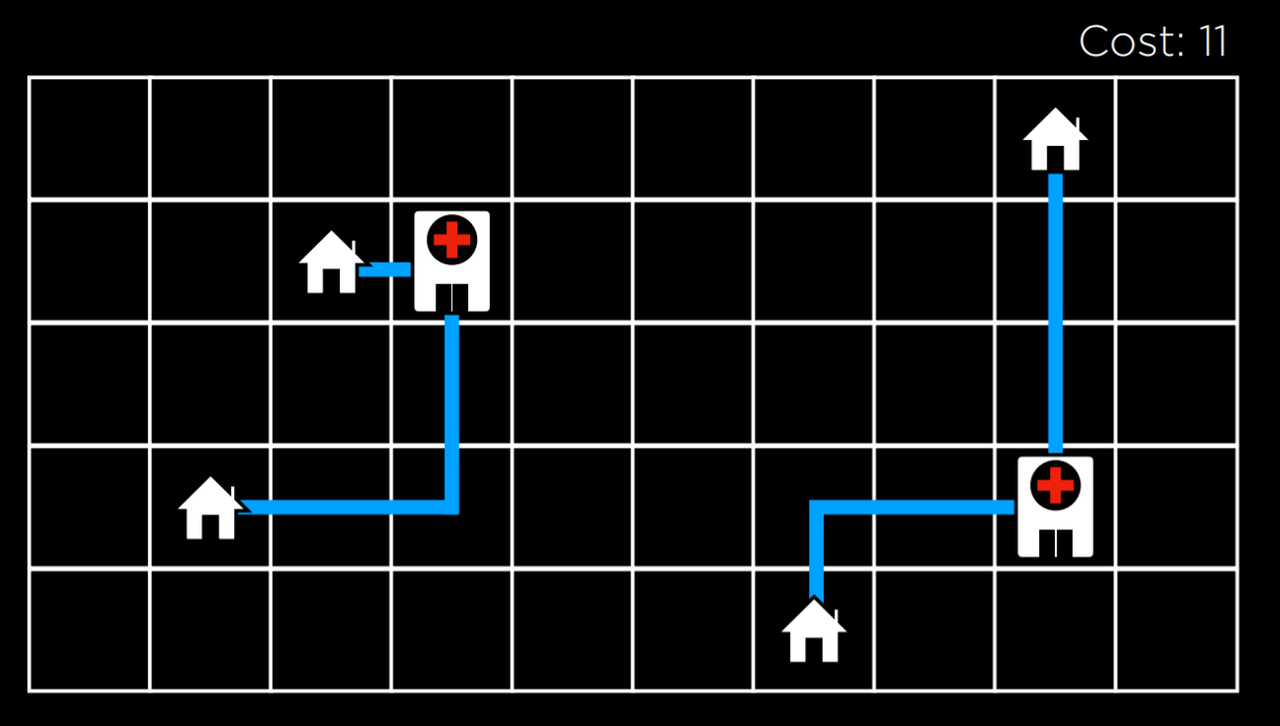
在这个状态下，成本是 11，比初始状态的成本 17 有所提高。然而，这还不是最佳状态。例如，将左边的医院移到左上角的房子下面，会使成本达到 9，比 11 好。然而，这个版本的爬山算法无法达到这个目标，因为所有的邻居状态都至少和当前状态的成本一样高。从这个意义上说，爬坡算法是短视的，它经常满足于比当下更好的解决方案，但不一定是所有可能的解决方案中最好的。

局部和全局最小值和最大值

如上所述，爬山算法可能卡在局部最大值或最小值中。局部最大值是一个比其相邻状态有更高值的状态。而全局最大值是指在状态空间的所有状态中具有最高值的状态。

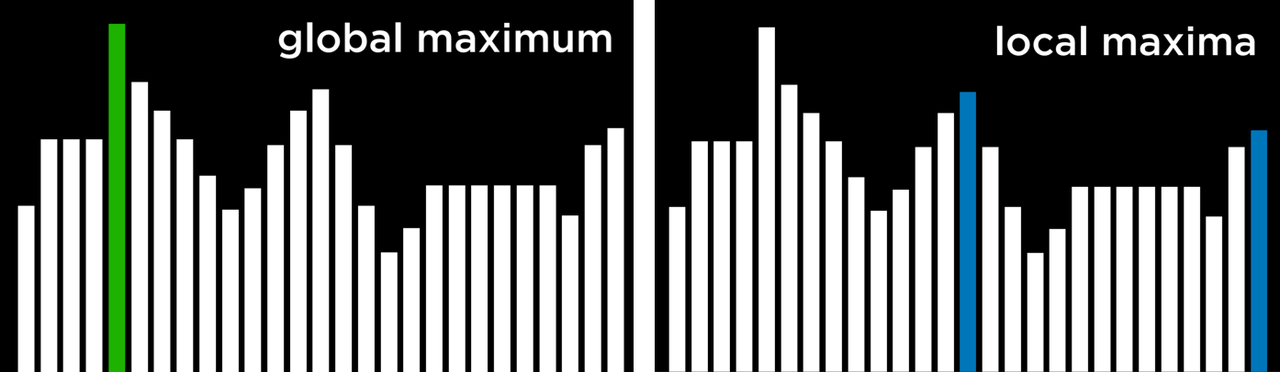
相比之下，局部最小值是一个比其相邻状态的值更低的状态。与此相对，全局最小值是指在状态空间中所有状态中具有最低值的状态。

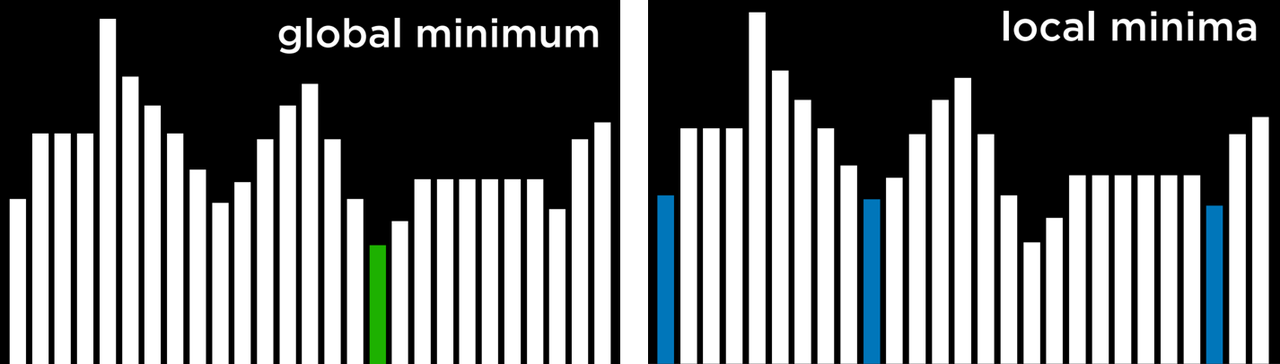
爬山算法的问题是，它们可能会在局部最小和最大中结束。一旦算法到达一个点，其邻居状态就目标函数而言，比当前状态更糟糕，算法就会停止。特殊类型的局部最大值和最小值包括平坦的局部最大值 / 最小值 (flat local maximum/minimum)，即多个数值相同的状态相邻，形成一个平原，从平原的中间开始，算法将无法向任何方向推进。

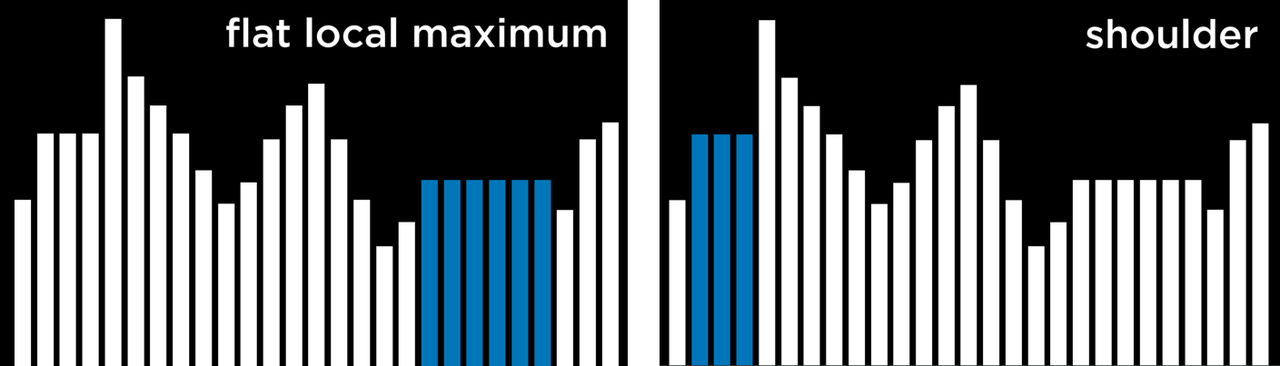
爬山算法的变体

由于爬山算法的局限性，人们想到了多种变体来克服卡在局部最小值和最大值的问题。该算法的所有变体的共同点是，无论采用何种策略，每一种变体都有可能陷入局部最小或最大，并且没有办法继续优化。下面的算法目标均是让数值越大越好（但它们也适用于成本函数，也就是使数值最小化，加一个负号即可互相转化）

Steepest-ascent: 选择值最高的邻居状态。
Stochastic: 从值较高的邻居状态中随机选择。这样做，我们选择去任何比我们的值更高的方向。
First-choice: 选择第一个值较高的邻居状态。
Random-restart: 进行多次爬山。每次都从一个随机状态开始。比较每次试验的最大值，并在这些最大值中选择一个。
Local Beam Search: 选择值最高的 k 个邻居状态。这与大多数本地搜索算法不同，它使用多个节点进行搜索，而不是只有一个节点。

虽然局部搜索算法并不总是给出最好的解决方案，但在考虑所有可能的状态在计算上不可行的情况下，它们往往能给出足够好的解决方案。

模拟退火算法 (Simulated Annealing)

尽管我们已经看到了可以改进爬山算法的变种，但它们都有一个共同的错误：一旦算法达到局部最大值，它就会停止运行。模拟退火算法允许算法在卡在局部最大值时 "摆脱" 自己。

退火是指加热金属并让其缓慢冷却的过程，其作用是使金属变硬。这被用来比喻模拟退火算法，该算法开始时温度较高，更有可能做出随机决定，也就是更可能选择比当前更差的邻居，随着温度的降低，它变得不太可能做出随机决定，越来越不可能选择比当前更差的邻居。这种机制允许算法将其状态改变为比当前状态更差的邻居状态，这就是它如何摆脱局部最大值的原因。以下是模拟退火法的伪代码：

txt

function Simulated-Annealing(problem, max):
    current = initial state of problem
    for t = 1 to max:
        T = Temperature(t)
        neighbor = random neighbor of current
        ΔE = how much better neighbor is than current
        if ΔE > 0:
            current = neighbor
        with probability e^(ΔE/T) set current = neighbor
    return current

该算法将一个 problem 和 max 作为输入， max 是它应该重复的次数。对于每个迭代， T 是用一个 Temperature 函数来设置的。这个函数在早期迭代中返回一个较高的值 (当 t 较低时)，在后期迭代中返回一个较低的值 (当 t 较高时)。然后，随机选择一个邻居状态，并计算 ΔE ，使其量化邻居状态比当前状态好的程度。如果邻居状态比当前状态好 ( ΔE>0 )，像以前一样，我们将当前状态设置为邻居状态。然而，当邻居状态较差时 ( ΔE<0 )，我们仍然可能将我们的当前状态设置为该邻居状态，并且我们以 $e^{Δ E / t}$ 的概率这样做。这里的意思是，更小的 ΔE ，更高的 t ，邻居状态被选择的概率越高 ( ΔE<0 )。这意味着邻居状态越好（虽然不如当下的状态），算法在其过程中越早，就越有可能将一个较差的邻居状态设置为当前状态。这背后的数学原理如下： e 是一个常数 (大约 2.72)， ΔE 是负数 (因为这个邻居比当前状态更糟糕)。温度 t 越高，ΔE/ t 就越接近于 0，使概率更接近于 1。

旅行商问题 (Traveling Salesman Problem)

在旅行商问题中，任务是连接所有的点，同时选择最短的距离。用离散数学的知识解释，也就是寻找一条权重最小的哈密尔顿图。例如，这就是快递公司需要做的事情：找到从商店到所有客户家的最短路线，然后再返回。

优化前	优化后

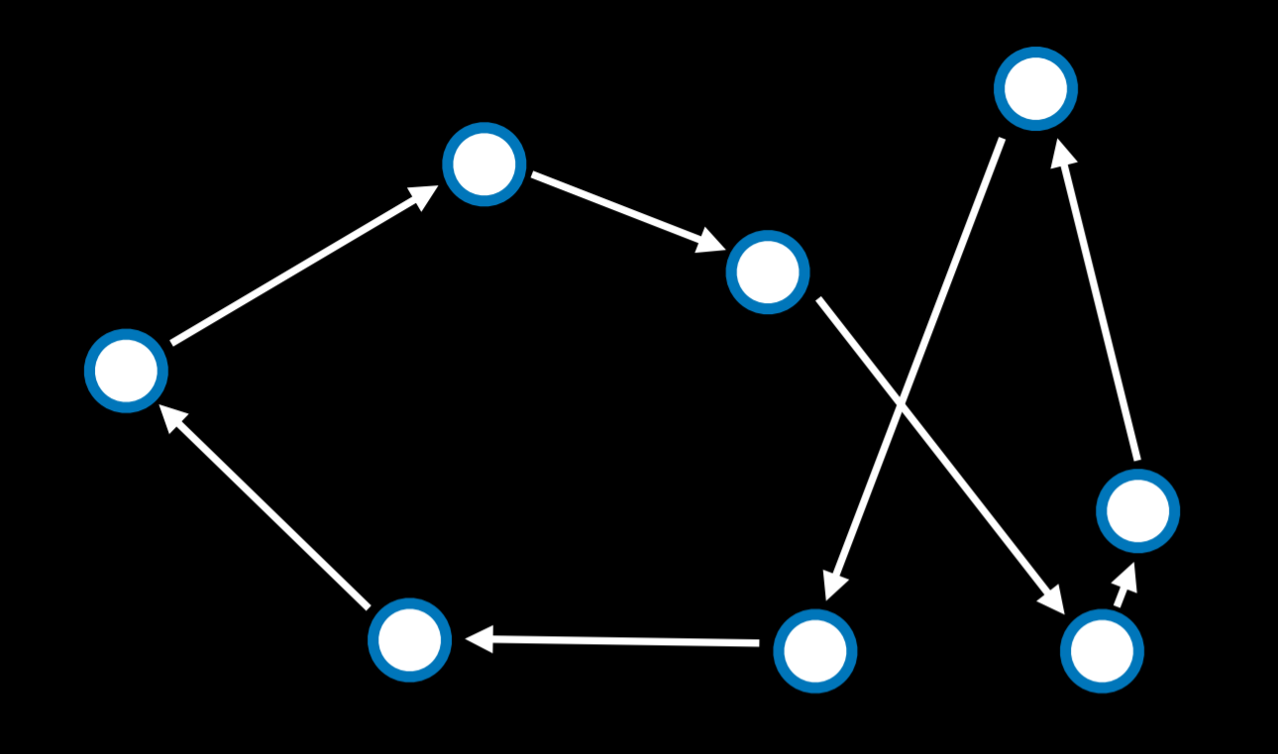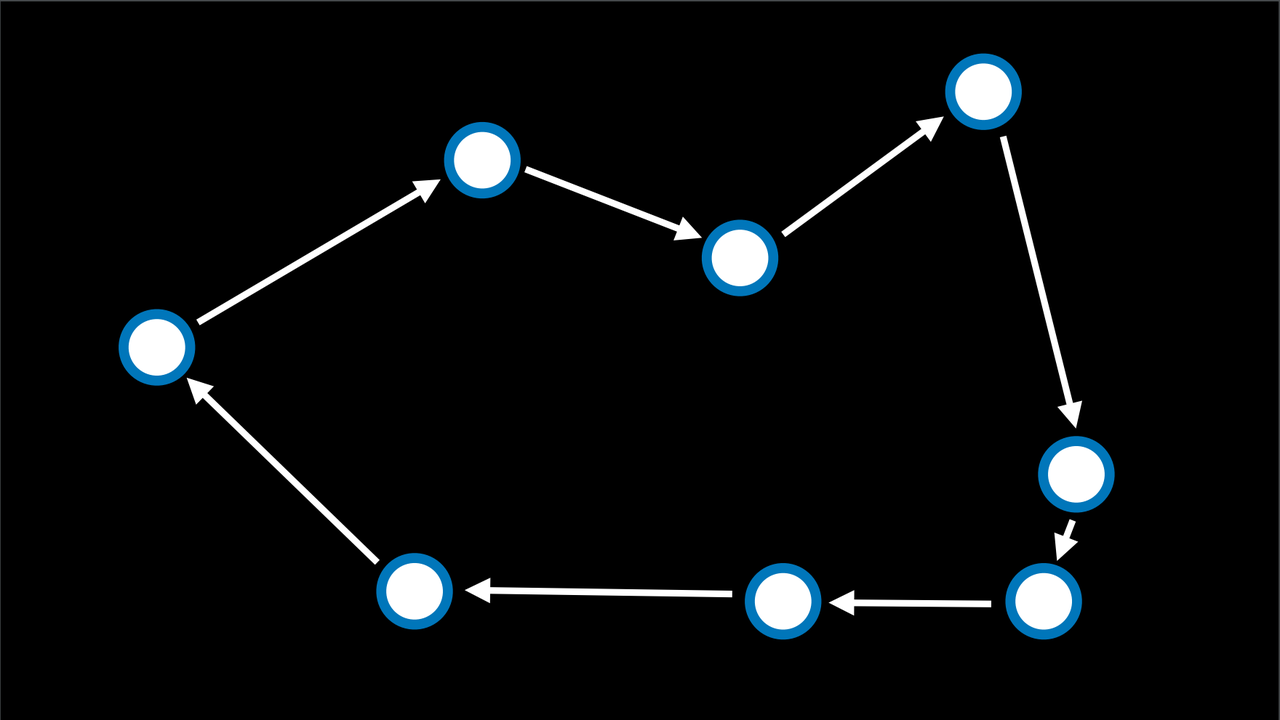在这种情况下，邻居状态可以被看作是两个箭头互换位置的状态。计算每一个可能的组合使得这个问题在计算上要求很高 (10 个点给了我们 10! 或者说 3,628,800 条可能的路线)。通过使用模拟退火算法，可以以较低的计算成本找到一个好的解决方案。

线性规划 (Linear Programming)

线性规划是一个优化线性方程 (y=ax₁+bx₂+... 形式的方程) 的问题系列。

线性规划有以下内容：

一个我们想要最小化的成本函数：c₁x₁ + c₂x₂ + ... + cₙxₙ。这里，每个 x 是一个变量，它与一些成本 c 相关联。
一个约束条件，它表示为一个变量的总和，它要么小于或等于一个值 (a₁x₁+a₂x₂+...+aₙxₙ≤b)，要么正好等于这个值 (a₁x₁+a₂x₂+...+aₙxₙ=b)。在这种情况下，x 是一个变量，a 是与之相关的一些资源，而 b 是我们可以为这个问题投入多少资源。
变量的域 (例如，一个变量不能是负数)，形式为 lᵢ≤xᵢ≤uᵢ。

请考虑以下例子：

两台机器，X₁和 X₂。X₁的运行成本为 50 美元 / 小时，X₂的运行成本为 80 美元 / 小时。我们的目标是使成本最小化。这可以被表述为一个成本函数：50x₁+80x₂。
X₁每小时需要 5 个单位的劳动力。X₂每小时需要 2 个单位的劳动力。总共需要花费 20 个单位的劳动力。这可以被形式化为一个约束条件：5x₁ + 2x₂ ≤ 20。
X₁每小时生产 10 个单位的产品。X₂每小时生产 12 个单位的产品。公司需要 90 个单位的产出。这是另一个约束条件。从字面上看，它可以被改写为 10x₁+12x₂≥90。然而，约束条件必须是 (a₁x₁+a₂x₂+...+aₙxₙ≤b) 或 (a₁x₁+a₂x₂+...+aₙxₙ=b)。因此，我们乘以 (-1)，得到一个所需形式的等价方程：(-10x₁)+(-12x₂)≤-90。

线性规划的优化算法需要几何学和线性代数的背景知识，而我们并不想假设这些知识。相反，我们可以使用已经存在的算法，如 Simplex 和 Interior-Point。

下面是一个使用 Python 中 scipy 库的线性规划例子：（此处用线性代数的知识会更好理解代码）

python

import scipy.optimize
# Objective Function: 50x_1 + 80x_2
# Constraint 1: 5x_1 + 2x_2 <= 20
# Constraint 2: -10x_1 + -12x_2 <= -90
result = scipy.optimize.linprog(
    [50, 80],  # Cost function: 50x_1 + 80x_2
    A_ub=[[5, 2], [-10, -12]],  # Coefficients for inequalities
    b_ub=[20, -90],  # Constraints for inequalities: 20 and -90
)
if result.success:
    print(f"X1: {round(result.x[0], 2)} hours")
    print(f"X2: {round(result.x[1], 2)} hours")
else:
    print("No solution")

约束满足 (Constraint Satisfaction)

约束满足问题是一类需要在满足某些条件下为变量赋值的问题。

约束条件满足问题具有一下特性:

变量集合 {x₁，x₂，...，xₙ}。
每个变量域的集合 {D₁, D₂, ..., Dₙ}。
一组约束条件 C

数独可以表示为一个约束满足问题，每个空方块是一个变量，域是数字 1-9，而约束是不能彼此相等的方块。

再考虑一个例子。每个学生 1-4 都在选修 A、B、...、G 中的三门课程。每门课程都需要有考试，可能的考试日是星期一、星期二和星期三。但是，同一个学生不能在同一天有两次考试。在这种情况下，变量是课程，域是天数，约束条件是哪些课程不能在同一天安排考试，因为是同一个学生在考试。这可以直观地显示如下：

这个问题可以用约束条件来解决，约束条件用图来表示。图中的每个节点是一门课程，如果两门课程不能安排在同一天，则在它们之间画一条边。在这种情况下，该图看起来是这样的：

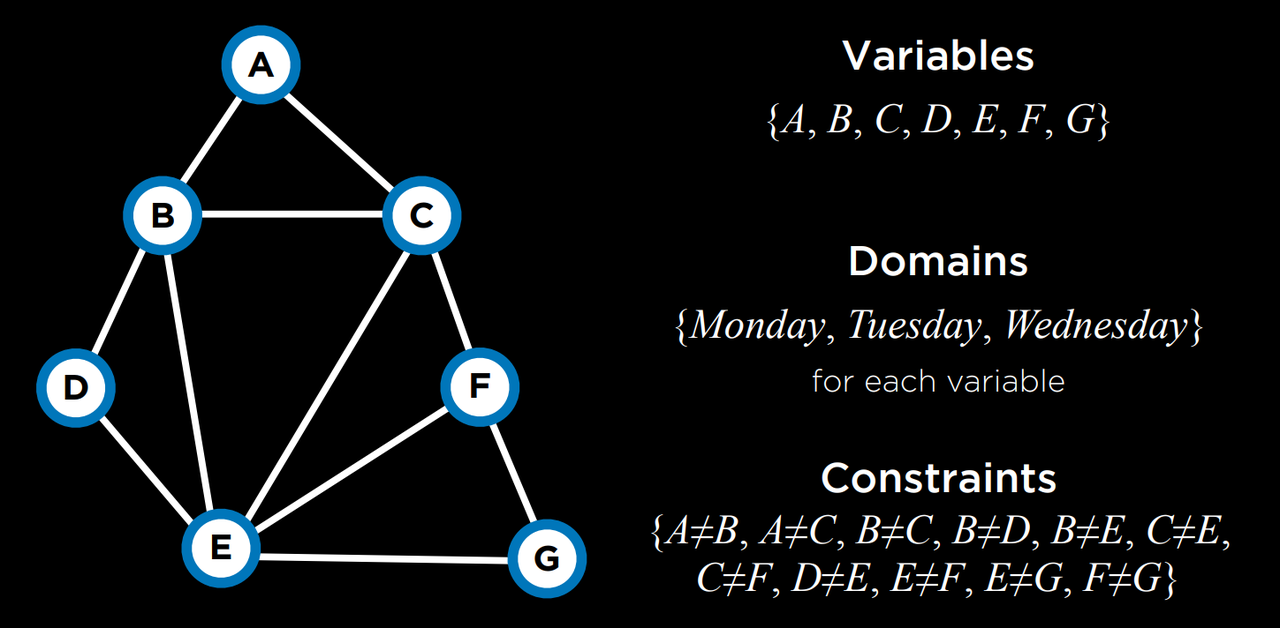
关于约束满足问题，还有几个值得了解的术语：

硬约束 (Hard Constraint) 是指在一个正确的解决方案中必须满足的约束。
软约束 (Soft Constraint) 用于表示哪种解决方案比其他解决方案更受欢迎。
一元约束 (Unary Constraint) 是指只涉及一个变量的约束。例如，课程 A 不能在周一有考试是一个一元约束 {A≠周一}。
二元约束 (Binary Constraint) 是一种涉及两个变量的约束。这就是我们在上面的例子中使用的约束类型，表示两个课程不能有相同的值 {A ≠ B}。

节点一致性 (Node Consistency)

节点一致性是指一个变量域中的所有值都满足该变量的一元约束。

例如，让我们拿两门课程，A 和 B。每门课程的域是 {Monday, Tuesday, Wednesday}，约束条件是 {A≠Mon，B≠Tue，B≠Mon，A≠B}。现在，A 和 B 都不是一致的，因为现有的约束条件使它们不能取其域中的每一个值。然而，如果我们从 A 的域中移除 Monday，那么它就会有节点一致性。为了实现 B 的节点一致性，我们必须从它的域中删除 Monday 和 Tuesday。

弧一致性 (Arc Consistency)

弧一致性是指一个变量域中的所有值都满足该变量的二元约束 (注意，我们现在用 "弧" 来指代我们以前所说的 "边")。换句话说，要使 X 对 Y 具有弧一致性，就要从 X 的域中移除元素，直到 X 的每个选择都对应的有 Y 的可能选择。

考虑到我们之前的例子，修改后的域：A:{Tuesday, Wednesday} 和 B:{Wednesday}。如果 A 与 B 是弧一致的，那么无论 A 的考试被安排在哪一天 (从它的域来看)，B 仍然能够安排考试。现在，A 与 B 是弧一致的吗？如果 A 取值为 Tuesday，那么 B 可以取值为 Wednesday。然而，如果 A 取值为 Wednesday，那么就没有 B 可以取的值 (记住，其中一个约束是 A≠B)。因此，A 与 B 不是弧一致的。为了改变这种情况，我们可以从 A 的域中删除 Wednesday。然后，A 的任何取值 (Tuesday 是唯一的选择) 都会给 B 留下一个取值 (Wednesday)。现在，A 与 B 是弧一致的。让我们看看一个伪代码的算法，使一个变量相对于其他变量是弧一致的 (注意，csp 代表 "约束满足问题")。

python

function Revise(csp, X, Y):
    revised = false
    for x in X.domain:
        if no y in Y.domain satisfies constraint for (X,Y):
            delete x from X.domain
            revised = true
    return revised

这个算法从跟踪 X 的域是否有任何变化开始，使用变量 revised，这在我们研究的下一个算法中会很有用。然后，代码对 X 的域中的每一个值进行重复，看看 Y 是否有一个满足约束条件的值。如果是，则什么都不做，如果不是，则从 X 的域中删除这个值。

通常情况下，我们感兴趣的是使整个问题的弧一致，而不仅仅是一个变量相对于另一个变量的一致性。在这种情况下，我们将使用一种叫做 AC-3 的算法，该算法使用 Revise：

python

function AC-3(csp):
    queue = all arcs in csp
    while queue non-empty:
        (X, Y) = Dequeue(queue)
        if Revise(csp, X, Y):
            if size of X.domain == 0:
                return false
            for each Z in X.neighbors - {Y}:
                Enqueue(queue, (Z,X))
    return true

该算法将问题中的所有弧添加到一个队列中。每当它考虑一个弧时，它就把它从队列中删除。然后，它运行 Revise 算法，看这个弧是否一致。如果做了修改使其一致，则需要进一步的行动。如果得到的 X 的域是空的，这意味着这个约束满足问题是无法解决的 (因为没有任何 X 可以取的值会让 Y 在约束条件下取任何值)。如果问题在上一步中没有被认为是不可解决的，那么，由于 X 的域被改变了，我们需要看看与 X 相关的所有弧是否仍然一致。也就是说，我们把除了 Y 以外的所有 X 的邻居，把他们和 X 之间的弧添加到队列中。然而，如果 Revise 算法返回 false，意味着域没有被改变，我们只需继续考虑其他弧。

虽然弧一致性的算法可以简化问题，但不一定能解决问题，因为它只考虑了二元约束，而没有考虑多个节点可能的相互连接方式。我们之前的例子中，4 个学生中的每个人都在选修 3 门课程，对其运行 AC-3 后，仍然没有变化。

我们讲过搜索问题。一个约束满足问题可以被看作是一个搜索问题：

初始状态 (Initial state)：空赋值 (所有变量都没有分配任何数值)。
动作 (Action)：在赋值中加入一个 {变量 = 值}；也就是说，给某个变量一个值。
过渡模型 (Transition model)：显示添加赋值如何改变变量。这没有什么深度：过渡模型返回包括最新动作后的整体的赋值的状态。
目标测试 (Goal test)：检查所有变量是否被赋值，所有约束条件是否得到满足。
路径成本函数 (Path cost function)：所有路径的成本都是一样的。正如我们前面提到的，与典型的搜索问题相比，优化问题关心的是解决方案，而不是通往解决方案的路线。

然而，把约束满足问题作为一个普通的搜索问题来处理，是非常低效的。相反，我们可以利用约束满足问题的结构来更有效地解决它。

回溯搜索 (Backtracking Search)

回溯搜索是一种考虑约束满足搜索问题结构的搜索算法。一般来说，它是一个递归函数，只要值满足约束，它就会尝试继续赋值。如果违反了约束，它将后退一步，尝试不同的赋值。让我们看看它的伪代码：

python

function Backtrack(assignment, csp):
    if assignment complete:
        return assignment
    var = Select-Unassigned-Var(assignment, csp)
    for value in Domain-Values(var, assignment, csp):
        if value consistent with assignment:
            add {var = value} to assignment
            result = Backtrack(assignment, csp)
            if result ≠ failure:
                return result
            remove {var = value} from assignment
    return failure

换句话说，如果当前赋值完成，则该算法返回当前赋值。这意味着，如果完成了算法，它将不会执行任何额外的操作，它只会返回已成立的赋值。如果赋值不完整，算法会从中选择一个尚未赋值的变量。然后，算法尝试为变量赋值，并对结果赋值再次运行回溯算法（递归）。然后，它检查结果值。如果不是失败，则表示赋值已完成，并且应返回此赋值。如果结果值失败，则删除最近的赋值，并尝试新的可能值，重复相同的过程。如果域中所有可能的值都返回失败，这意味着我们需要回溯。也就是说，问题出在之前的一些步骤上。如果这种情况发生在我们第一个考虑的变量上，我们无法往后了，那么这意味着没有解决方案满足约束。

考虑以下行动方案：

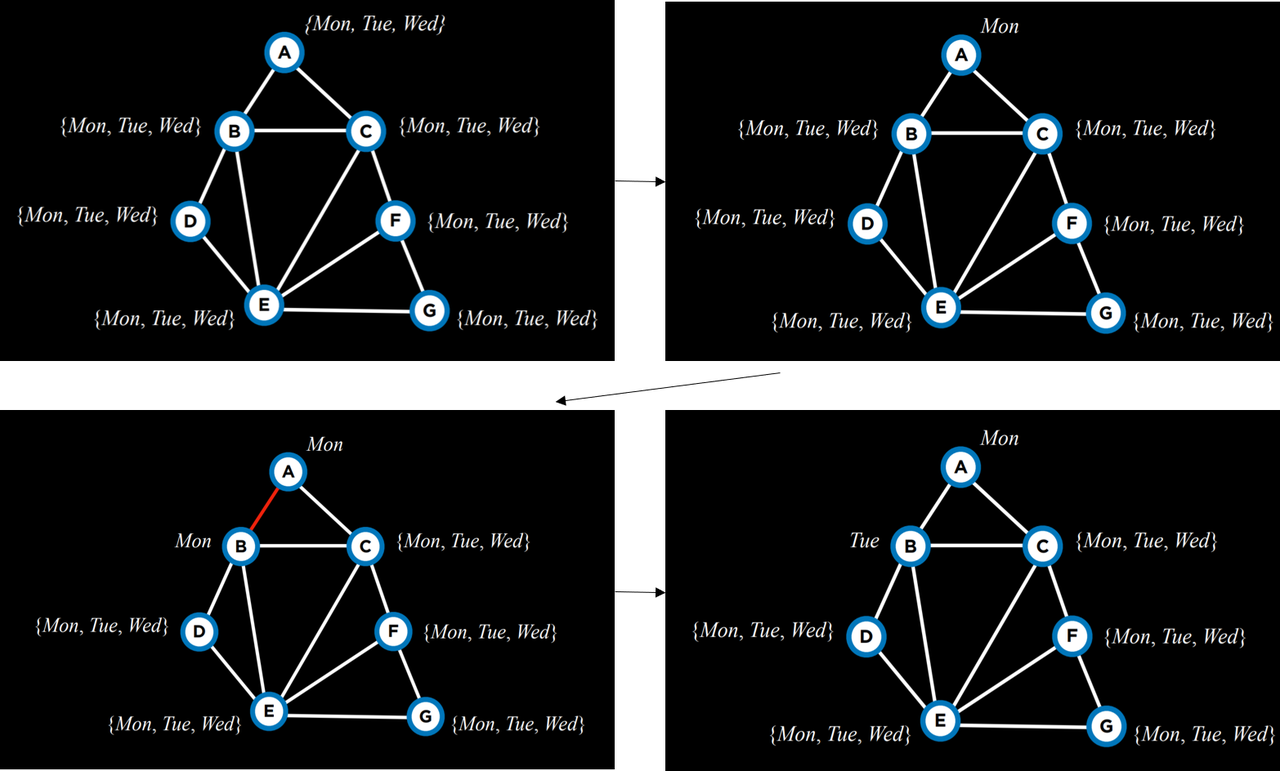
我们从空赋值开始。然后，我们选择变量 A，并给它赋值 Mon 。然后，使用这个赋值，我们再次运行算法。既然 A 已经有了一个赋值，算法将考虑 B，并将 Mon 赋值给它。此赋值返回 false ，因此算法将尝试在 Tue 为 B 赋值，而不是在给定上一个赋值的情况下为 C 赋值。这个新的赋值满足约束条件，在给定这个赋值的情况下，下一步将考虑一个新的变量。例如，如果将 Tue 或 Wed 也赋值给 B 会导致失败，那么算法将回溯并返回到考虑 A，为其分配另一个值，即 Tue 。如果 Tue 和 Wed 也失败了，那么这意味着我们已经尝试了所有可能的赋值，该问题是无法解决的。

在源代码部分，您可以从头开始实现的回溯算法。然而，这种算法被广泛使用，因此，多个库已经包含了它的实现。

推理 (Inference)

尽管回溯搜索比简单搜索更有效，但它仍然需要大量的算力。另一方面，满足弧一致性需要的算力较低。通过将回溯搜索与满足弧一致性（也就是推理）交织在一起，我们可以得到一种更有效的算法。该算法被称为 “保持弧一致性”(Maintaining Arc-Consistency) 算法。该算法将在每次新的回溯搜索分配之后重新调整变量的域，使得满足弧一致性。具体来说，在我们对 X 进行新的赋值后，我们将调用 AC-3 算法，并从所有弧 (Y，X) 的队列开始，其中 Y 是 X 的邻居 (而不是问题中所有弧的队列)。以下是一个经过修订的 Backtrack 算法，该算法保持了弧的一致性。

python

function Backtrack(assignment, csp):
    if assignment complete:
        return assignment
    var = Select-Unassigned-Var(assignment, csp)
    for value in Domain-Values(var, assignment, csp):
        if value consistent with assignment:
            add {var = value} to assignment            # new here
            inferences = Inference(assignment, csp)    # new here
            if inferences ≠ failure:
                add inferences to assignment
            result = Backtrack(assignment, csp)
            if result ≠ failure:
                return result
            remove {var = value} and inferences from assignment    # new here
    return failure

Inference 函数运行 AC-3 算法，如前所述。它的输出是满足弧一致性的变量域。从字面上看，这些是可以从以前的赋值和约束满足问题的结构中推导出来的新变量域。

还有其他方法可以提高算法的效率。到目前为止，我们随机选择了一个未分配的变量。然而，有些选择比其他选择更有可能更快地找到解决方案。这需要使用启发式方法。启发式是一条经验法则，这意味着，通常情况下，它会比遵循随机的方法带来更好的结果，但不能保证总是更优。

最小剩余值 (Minimum Remaining Values (MRV)) 就是这样一种启发式方法。这里的想法是，如果一个变量的域被推理限制了，现在它只剩下一个值 (或者两个值)，也就是可取的范围比较小，那么通过进行这种赋值，我们以后可能需要进行的回溯次数会比较少。也就是说，我们迟早要做这个赋值，因为它是从满足弧一致性中推断出来的。如果这项任务失败了，最好尽快发现，避免以后的回溯。

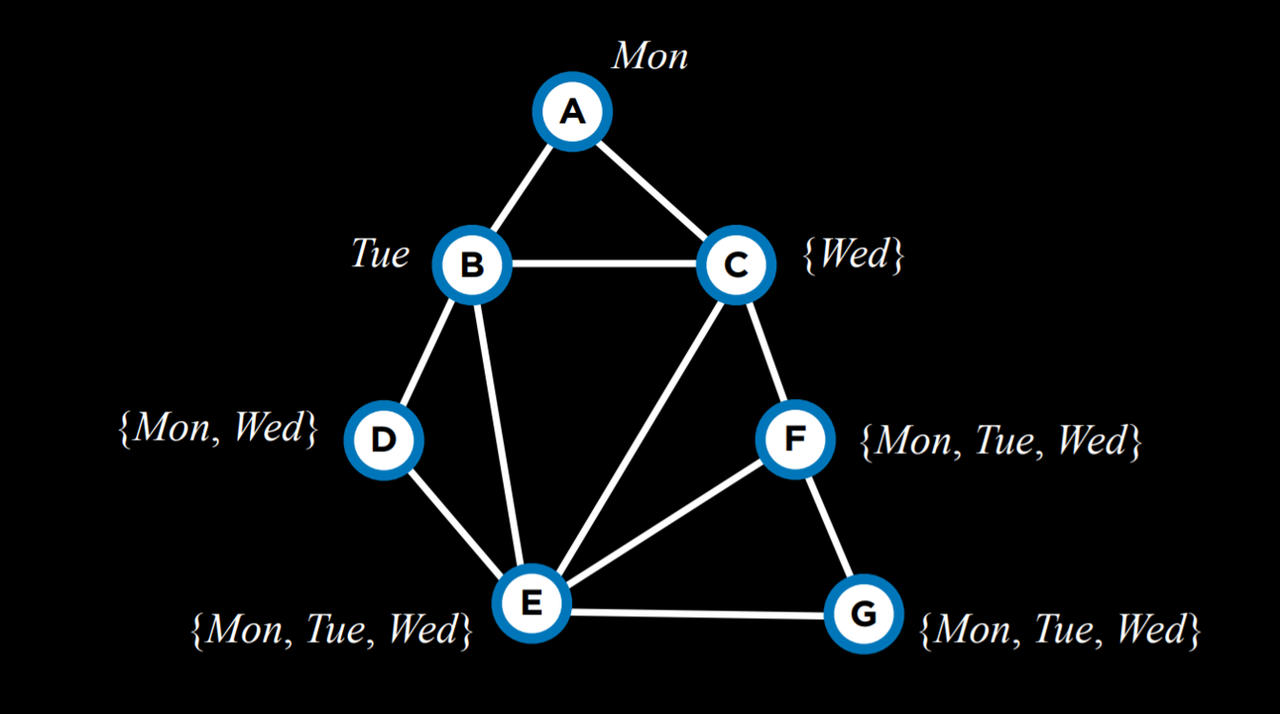
例如，在给定当前赋值的情况下缩小变量的域后，使用 MRV 启发式，我们接下来将选择变量 C，并以 Wed 为其赋值，因为 C 的取值可能性是最少的。

度 (Degree) 启发式依赖于变量的度，其中度是指将一个变量连接到几个其他变量。通过一次赋值选择度最高的变量，我们约束了多个其他变量，从而加快了算法的进程。

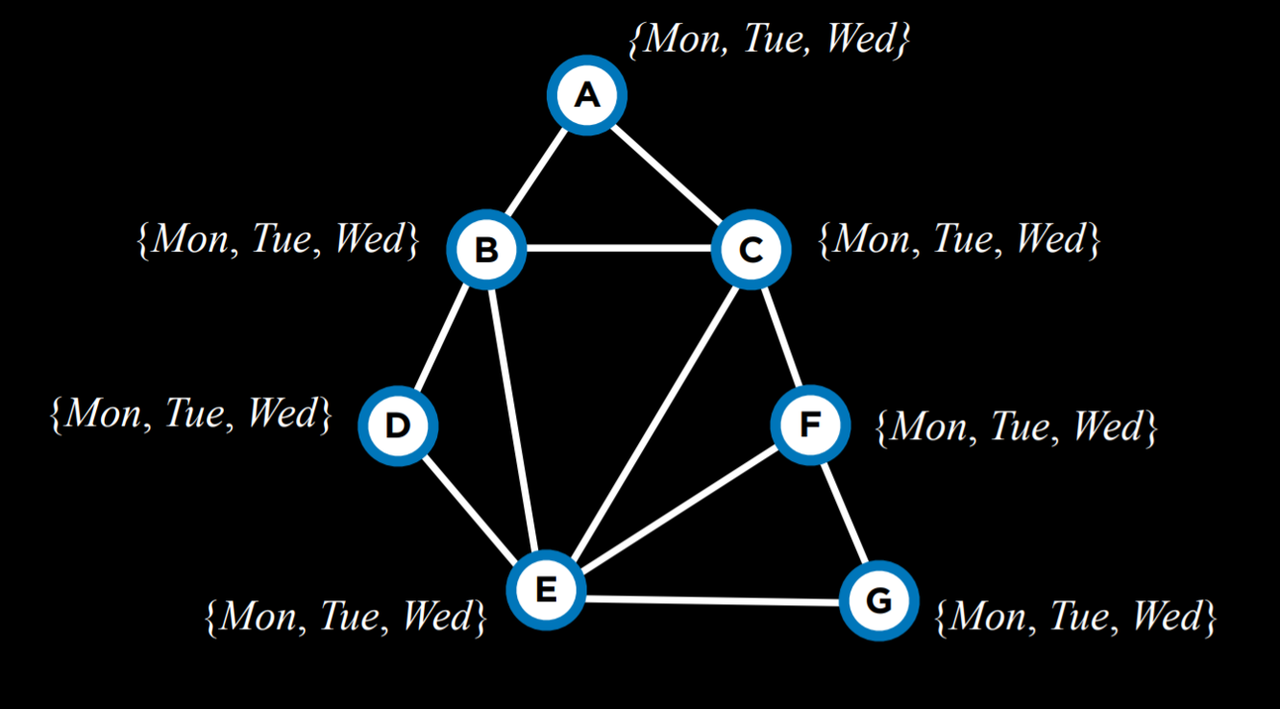
例如，上面所有的变量都有相同大小的域。因此，我们应该选择一个度最高的域，它将是变量 E。

这两种启发式方法并不总是适用的。例如，当多个变量的可取值数量具有相同的最小值时，或者当多个变量的度具有相同的最大值时。

另一种提高算法效率的方法是， 最小约束值 (Least Constraining Values) 启发式，在这里我们选择将约束最少其他变量的值。这里的想法是，在度启发式中，我们希望使用更可能约束其他变量的变量，而在这里，我们希望这个变量在取值之后对其他变量的约束最少。也就是说，我们希望找到可能是最大潜在麻烦源的变量 (度最高的变量)，然后使其尽可能不麻烦 (为其赋值约束其他变量最少的值)。

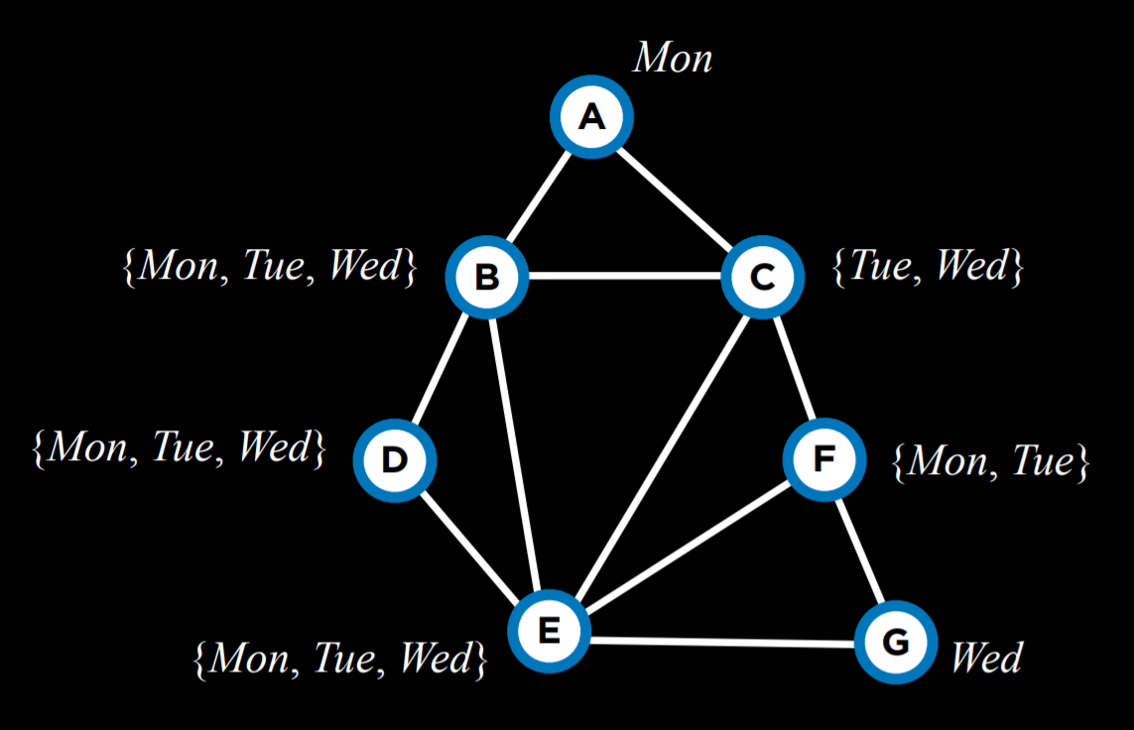
例如，让我们考虑变量 C。如果我们将 Tue 分配给它，我们将对所有 B、E 和 F 施加约束。然而，如果我们选择 Wed ，我们将只对 B 和 E 施加约束。因此，选择 Tue 可能更好。

总之，优化问题可以用多种方式来表述。在这，我们考虑了局部搜索、线性规划和约束满足。

3.6.2搜索

3.6.3知识推理

3.6.4不确定性问题

3.6.5最优化

3.7.2Prerequisites

3.7.3Ray Tracing

3.8.4Numpy&Pytorch系列

3.8.5LLM实操项目

3.8.5.2Atri-微调角色扮演

3.8.5.3AI绘图大模型-Stable Diffusion

3.8.5.4语音识别-Whisper + Gradio部署

3.8.5.5微调Llama 2

最优化

局部搜索 (Local Search)

爬山算法 (Hill Climbing)

局部和全局最小值和最大值

爬山算法的变体

模拟退火算法 (Simulated Annealing)

旅行商问题 (Traveling Salesman Problem)

线性规划 (Linear Programming)

约束满足 (Constraint Satisfaction)

节点一致性 (Node Consistency)

弧一致性 (Arc Consistency)

回溯搜索 (Backtracking Search)

推理 (Inference)

3.8.5.2Atri-微调角色扮演

3.8.5.3AI绘图大模型-Stable Diffusion

3.8.5.4语音识别-Whisper + Gradio部署

3.8.5.5微调Llama 2

最优化 ​

局部搜索 (Local Search) ​

爬山算法 (Hill Climbing) ​

局部和全局最小值和最大值 ​

爬山算法的变体 ​

模拟退火算法 (Simulated Annealing) ​

旅行商问题 (Traveling Salesman Problem) ​

线性规划 (Linear Programming) ​

约束满足 (Constraint Satisfaction) ​

节点一致性 (Node Consistency) ​

弧一致性 (Arc Consistency) ​

回溯搜索 (Backtracking Search) ​

推理 (Inference) ​

最优化

局部搜索 (Local Search)

爬山算法 (Hill Climbing)

局部和全局最小值和最大值

爬山算法的变体

模拟退火算法 (Simulated Annealing)

旅行商问题 (Traveling Salesman Problem)

线性规划 (Linear Programming)

约束满足 (Constraint Satisfaction)

节点一致性 (Node Consistency)

弧一致性 (Arc Consistency)

回溯搜索 (Backtracking Search)

推理 (Inference)